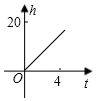
 B .
B . 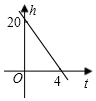 C .
C . 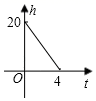 D .
D . 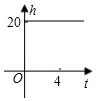
| x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| y/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
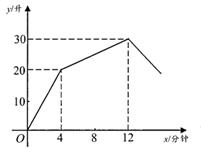
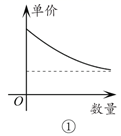
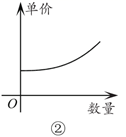
下列说法错误的是( )
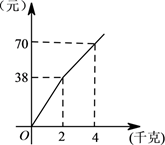

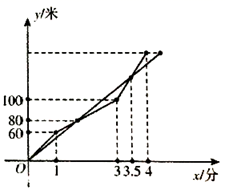
①两个机器人第一次相遇时间是在第2分钟;
②小 每分钟跑50米;
③赛程总长200米;
④小 到达终点的时候小
距离终点还有20米.