北京市丰台区2020年中考数学二模试卷

更新时间：2020-07-17 浏览次数：334 类型：中考模拟

一、单选题

1. (2020·丰台模拟) 下图是某个几何体的展开图，该几何体是（）

A . 三棱柱 B . 三棱锥 C . 圆柱 D . 圆锥

答案解析收藏纠错 + 选题
2. (2023八上·昆明期中) 熔喷布，俗称口罩的“心脏”，是口罩中间的过滤层，能过滤细菌，阻止病菌传播．经测量，医用外科口罩的熔喷布厚度约为0.000156米，将0.000156用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·深圳模拟) 实数a，b，c在数轴上的对应点的位置如图所示，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020·丰台模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，如果 $\text{[math]}$ 平分 $\text{[math]}$ ，那么 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九下·乳山期中) 如果 $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值为（）

A . 12 B . 6 C . 2 D . -6

答案解析收藏纠错 + 选题
6. (2024九下·越秀模拟) 一组数据1，2，2，3，5，将这组数据中的每一个数都加上 $\text{[math]}$ ，得到一组新数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，这两组数据的以下统计量相等的是（）

A . 平均数 B . 众数 C . 中位数 D . 方差

答案解析收藏纠错 + 选题
7. (2022九上·杭州月考) 如图，点A，B是 $\text{[math]}$ 上的定点，点P为优弧 $\text{[math]}$ 上的动点（不与点A，B重合），在点P运动的过程中，以下结论正确的是（）

A . $\text{[math]}$ 的大小改变 B . 点P到弦 $\text{[math]}$ 所在直线的距离存在最大值 C . 线段 $\text{[math]}$ 与 $\text{[math]}$ 的长度之和不变 D . 图中阴影部分的面积不变

答案解析收藏纠错 + 选题
8. (2021九下·乳山期中) 如图，抛物线 $\text{[math]}$ ．将该抛物线在x轴和x轴下方的部分记作 $\text{[math]}$ ，将 $\text{[math]}$ 沿x轴翻折记作 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 构成的图形记作 $\text{[math]}$ ．关于图形 $\text{[math]}$ ，给出如下四个结论，其中错误的是（）

A . 图形 $\text{[math]}$ 恰好经过4个整点（即横、纵坐标均为整数的点） B . 图形 $\text{[math]}$ 上任意一点到原点的距离都不超过1 C . 图形 $\text{[math]}$ 的周长大于 $\text{[math]}$ D . 图形 $\text{[math]}$ 所围成的区域的面积大于2且小于 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2020·丰台模拟) 如图，已知 $\text{[math]}$ ，用量角器度量 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
10. (2021·长春) 不等式组 $\text{[math]}$ 的所有整数解是．

答案解析收藏纠错 + 选题
11. (2020八下·泰兴期末) 一个不透明的盒子中装有3个黄球，6个红球，这些球除了颜色外无其他差别．从中随机摸出一个球，恰好是黄球的概率为．

答案解析收藏纠错 + 选题
12. (2020七下·厦门期末) 小明把一副三角板摆放在桌面上，如图所示，其中边 $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上，可以得到//，依据是．

答案解析收藏纠错 + 选题
13. (2020·丰台模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 于点E．如果 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
14. (2020·丰台模拟) 如图，正比例函数 $\text{[math]}$ 的图象和反比例函数 $\text{[math]}$ 的图象交于A，B两点，分别过点A，B作 $\text{[math]}$ 轴的垂线，垂足为点C，D，则△ $\text{[math]}$ 与 $\text{[math]}$ 的面积之和为．

答案解析收藏纠错 + 选题
15. (2020·丰台模拟) 经济学家在硏究市场供求关系时，一般用纵轴表示产品单价（自变量），而用横轴表示产品数量（因变量），下列两条曲线分别表示某种产品数量与单价之间的供求关系，一条表示厂商希望的供应曲线，另一条表示客户希望的需求曲线，其中表示客户希望的需求曲线的是（填入序号即可）．

答案解析收藏纠错 + 选题
16. (2020·丰台模拟) 小志自主创业，在网上经营一家水果店，销售的水果中有盒装草莓、荔枝、山竹，价格依次为40元/盒、60元/盒、80元/盒．为增加销量，小志对这三种水果进行促销：一次性购买水果的总价超过100元时，超过的部分打5折，每笔订单限购3盒．顾客支付成功后，小志会得到支付款的80%作为货款．
1. （1）顾客一笔订单购买了上述三种水果各一盒，则小志收到的货款是元；
2. （2）小志在两笔订单中共售出原价180元的水果，则他收到的货款最少是元．
答案解析收藏纠错 + 选题

三、解答题

17. (2020·丰台模拟) 下面是小文设计的“过圆外一点作圆的切线”的作图过程．已知： $\text{[math]}$ 和圆外一点P．求作：过点P的 $\text{[math]}$ 的切线．作法：①连接 $\text{[math]}$ ；②以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，交 $\text{[math]}$ 于点A，B；③作直线 $\text{[math]}$ ， $\text{[math]}$ ；所以直线 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的切线．

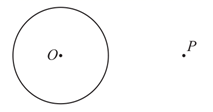
根据小文设计的作图过程，完成下面的证明．

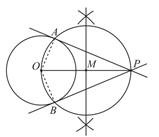
证明：连接 $\text{[math]}$ ， $\text{[math]}$ ．

∵ $\text{[math]}$ 为 $\text{[math]}$ 的直径，

∴ $\text{[math]}$ =∠     ▲      = ▲   º

（ ▲   ）（填推理的依据）．

∴ $\text{[math]}$ ， ▲   $\text{[math]}$ ．

∵ $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的半径，

∴直线 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的切线（ ▲   ）（填推理的依据）．

答案解析收藏纠错 + 选题
18. (2024九下·北京市模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2021·陕西模拟) 解分式方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2021·龙门模拟) 关于x的方程 $\text{[math]}$ ．
1. （1）求证：方程总有两个实数根；
2. （2）请你选择一个合适的m的值，使得方程的两个根都是整数，并求此时方程的根．
答案解析收藏纠错 + 选题
21. (2020八下·韩城期末) 如图，矩形 $\text{[math]}$ ，延长 $\text{[math]}$ 至点E，使 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，过点C作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点F，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G．当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2020·丰台模拟) 在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 和点B，与 $\text{[math]}$ 轴交于点C．
1. （1）求k的值；
2. （2）如果 $\text{[math]}$ ，求一次函数的表达式．
答案解析收藏纠错 + 选题
23. (2020·丰台模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，C为 $\text{[math]}$ 延长线上一点， $\text{[math]}$ 为 $\text{[math]}$ 的切线，切点为D， $\text{[math]}$ 于点E，且 $\text{[math]}$ 与 $\text{[math]}$ 交于点F．
1. （1）求证：点D为 $\text{[math]}$ 的中点；
2. （2）如果 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

24. (2020·丰台模拟) 2020年3月至5月，某校开展了一系列居家阅读活动．学生利用“宅家”时光，在书海中遨游，从阅读中获得精神慰藉和自我提升．为了解学生居家阅读的情况，学校从七、八两个年级各随机抽取50名学生，进行了居家阅读情况调查．下面给出了部分数据信息：

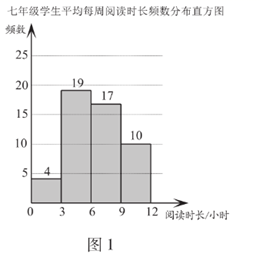
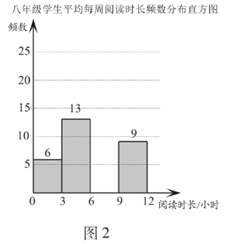
$\text{[math]}$ ．两个年级学生平均每周阅读时长 $\text{[math]}$ （单位：小时）的频数分布直方图如下（数据分成4组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）：

b．七年级学生平均每周阅读时长在 $\text{[math]}$ 这一组的是：6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8

c．两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下：

	平均数	中位数	众数	方差
七年级	6.3	m	8	7.0
八年级	6.0	7	7	6.3

根据以上信息，回答下列问题：

（1）补全图2；
（2）写出表中m的值；
（3）返校后，学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号．小丽说：“根据频数分布直方图中的数据信息，估计七年级约有20%的学生获得该称号，八年级约有18%的学生获得该称号，所以七年级获得该称号的人数一定比八年级获得该称号的人数多．”你认为她的说法（填入“正确”或“不正确”）；
（4）请你结合数据对两个年级的居家阅读情况进行评价．

答案解析收藏纠错 + 选题

25. (2020·丰台模拟) 小腾的爸爸计划将一笔资金用于不超过10天的短期投资，针对这笔资金，银行专属客户经理提供了三种投资方案，这三种方案的回报如下：

方案一：每一天回报30元；

方案二：第一天回报8元，以后每一天比前一天多回报8元；

方案三：第一天回报0.5元，以后每一天的回报是前一天的2倍．

下面是小腾帮助爸爸选择方案的探究过程，请补充完整：

（1）确定不同天数所得回报金额（不足一天按一天计算），如下表：

天数	1	2	3	4	5	6	7	8	9	10
方案一	30	30	30	30	30	30	30	30	30	30
方案二	8	16	24	32	40	48	56	64	72	80
方案三	0.5	1	2	4	8	16	32	64	128	$\text{[math]}$

其中 $\text{[math]}$ ；

（2）计算累计回报金额，设投资天数为x（单位：天），所得累计回报金额是y（单位：元），于是得到三种方案的累计回报金额 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与投资天数x的几组对应值：

$\text{[math]}$	1	2	3	4	5	6	7	8	9	10
$\text{[math]}$	30	60	90	120	150	180	210	240	270	300
$\text{[math]}$	8	24	48	80	120	168	224	288	360	440
$\text{[math]}$	0.5	1.5	3.5	7.5	15.5	31.5	63.5	127.5	255.5	$\text{[math]}$

其中 $\text{[math]}$ ；

（3）在同一平面直角坐标系 $\text{[math]}$ 中，描出补全后的表中各组数值所对应的点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，并画出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的图象；

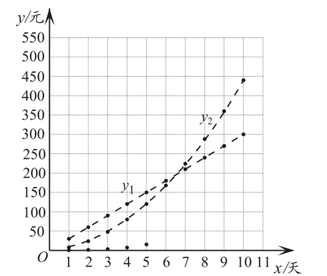
注：为了便于分析，用虚线连接离散的点．
（4）结合图象，小腾给出了依据不同的天数而选择对应方案的建议：

答案解析收藏纠错 + 选题

26. (2020·丰台模拟) 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点A．
1. （1）求点A的坐标（用含 $\text{[math]}$ 的式子表示）；
2. （2）求抛物线与x轴的交点坐标；
3. （3）已知点 $\text{[math]}$ ， $\text{[math]}$ ，如果抛物线与线段 $\text{[math]}$ 恰有一个公共点，结合函数图象，求a的取值范围．
答案解析收藏纠错 + 选题
27. (2020·丰台模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转45°，得到 $\text{[math]}$ ，点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，连接 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）根据题意补全图形；
2. （2）判断 $\text{[math]}$ 的形状，并证明；
3. （3）连接 $\text{[math]}$ ，用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并证明．
  温馨提示：在解决第（3）问的过程中，如果你遇到困难，可以参考下面几种解法的主要思路．
  
  解法1的主要思路：
  
  延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，可证 $\text{[math]}$ ，再证 $\text{[math]}$ 是等腰直角三角形．
  
  解法2的主要思路：
  
  过点A作 $\text{[math]}$ 于点M，可证 $\text{[math]}$ 是等腰直角三角形，再证 $\text{[math]}$ ．
  
  解法3的主要思路：
  
  过点A作 $\text{[math]}$ 于点M，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点N，设 $\text{[math]}$ ， $\text{[math]}$ ，用含a或b的式子表示 $\text{[math]}$ ， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
28. (2020·丰台模拟) 过直线外一点且与这条直线相切的圆称为这个点和这条直线的点线圆．特别地，半径最小的点线圆称为这个点和这条直线的最小点线圆．
在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ．
1. （1）已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，分别以A，B为圆心，1为半径作 $\text{[math]}$ ， $\text{[math]}$ ，以C为圆心，2为半径作 $\text{[math]}$ ，其中是点P和x轴的点线圆的是；
2. （2）记点P和x轴的点线圆为 $\text{[math]}$ ，如果 $\text{[math]}$ 与直线 $\text{[math]}$ 没有公共点，求 $\text{[math]}$ 的半径r的取值范围；
3. （3）直接写岀点P和直线 $\text{[math]}$ 的最小点线圆的圆心的横坐标t的取值范围．
答案解析收藏纠错 + 选题