
 B .
B . 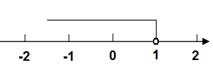 D .
D . 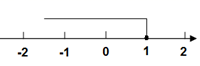




七年级:88 94 90 94 84 94 99 94 99 100
八年级:84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:
|
成绩x 人数 年级 |
80≤x<85 |
85≤x<90 |
90≤x<95 |
95≤x≤100 |
|
七年级 |
1 |
1 |
5 |
3 |
|
八年级 |
a |
1 |
4 |
4 |
分析数据:补全下列表格中的统计量:
|
统计量 年级 |
平均数 |
中位数 |
众数 |
方差 |
|
七年级 |
93.6 |
94 |
b |
24.2 |
|
八年级 |
93.7 |
c |
93 |
20.4 |
得出结论:


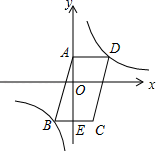
步骤一:利用三角板上的刻度,在OA、OB上分别截取OM、ON,使OM=ON.
步骤二:分别过点M、N作OM、ON的垂线,交于点P.
步骤三:作射线OP,则OP为∠AOB的平分线.
①请写出小明作法的完整证明过程.
②当tan∠AOB= 时,量得MN=4cm,直接写出
的面积.

