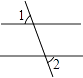
 B .
B .  C .
C . 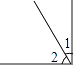 D .
D . 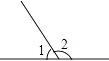


 B .
B .  C .
C .  D .
D . 

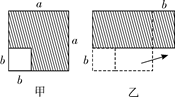


如图,已知AB∥CE,∠A=∠E,试说明:∠CGD=∠FHB.

解:因为AB∥CE(已知),
所以∠A=∠ ▲ ( ▲ ).
因为∠A=∠E(已知),
所以∠ ▲ =∠ ▲ (等量代换).
所以 ▲ ∥ ▲ ( ▲ ).
所以∠CGD=∠ ▲ ( ▲ ).
因为∠FHB=∠GHE( ▲ ),
所以∠CGD=∠FHB(等量代换).
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律!

如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)0=1.它只有一项,系数为1;
(a+b)1=a+b展开式中的系数1、1恰好对应图中第二行的数字;
(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;
(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.

