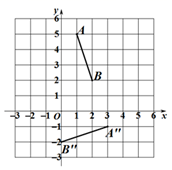
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 


|
组别 |
学习时间x(h) |
人数(人) |
|
A |
2.5<x≤3 |
40 |
|
B |
3<x≤3.5 |
170 |
|
C |
3.5<x≤4 |
350 |
|
D |
4<x≤4.5 |
|
|
E |
4.5<x≤5 |
90 |
|
F |
5小时以上 |
50 |




