河南省2021年数学中考三模试卷

更新时间：2021-05-20 浏览次数：298 类型：中考模拟

一、单选题

1. (2021·河南模拟) 比﹣4.5小的负整数是（）

A . ﹣3 B . ﹣5.5 C . ﹣5 D . 0

答案解析收藏纠错 + 选题
2. (2024七下·温县期中) 某种芯片每个探针单元的面积为 $\text{[math]}$ ，0.00000164用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·河南模拟) 如图，已知直线AD，BE，CF相交于点O，OG $\text{[math]}$ AD，且 $\text{[math]}$ BOC=35°， $\text{[math]}$ FOG=30°，则 $\text{[math]}$ DOE的度数为（）

A . 30° B . 35° C . 15° D . 25°

答案解析收藏纠错 + 选题
4. (2024八下·浦东期末) 已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）

A . ∠A=∠B B . ∠A=∠C C . AC=BD D . AB⊥BC

答案解析收藏纠错 + 选题
5. (2021八下·邯山期末) 如图是小颖前三次购买苹果单价的统计图，第四次又买的苹果单价是a元/千克，发现这四个单价的中位数恰好也是众数，则a=（）

A . 9 B . 8 C . 7 D . 6

答案解析收藏纠错 + 选题
6. (2021·河南模拟) 小敏计划在暑假参加海外游学，她打算制作一个正方体礼盒送给外国朋友.如图所示是她设计的礼盒的平面展开图，请你判断，正方体礼盒上与“孝”字相对的面上的字是（）

A . 义 B . 仁 C . 智 D . 信

答案解析收藏纠错 + 选题
7. (2021·河南模拟) 《九章算术》是中国古代的数学专著，奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就. 《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三.问人数、羊价各几何？”译文：“假设有若干人共同出钱买羊，如果每人出5钱，那么还差45钱；如果每人出7钱，那么仍旧差3钱，求买羊的人数和羊的价钱.”设羊是x钱，可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·西岗月考) 在二次函数y＝－x²＋bx＋c中，函数y与自变量x的部分对应值如下表：

x

……

－2

0

3

4

……

y

……

－7

m

n

－7

……

则m、n的大小关系为（）

A . m＞n B . m＜n C . m＝n D . 无法确定

答案解析收藏纠错 + 选题
9. (2021·河南模拟) 如图，把△ABC沿着BC的方向平移到△DEF的位置，它们重叠部分的面积是△ABC面积的一半，若BC＝ $\text{[math]}$ ，则△ABC移动的距离是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·河南模拟) 如图，弹性小球从点P（0，1）出发，沿所示方向运动，每当小球碰到正方形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到正方形的边时的点为P₁（2，0），第2次碰到正方形的边时的点为P₂ ， …，第n次碰到正方形的边时的点为P_n ，则点P₂₀₁₈的坐标是（）

A . （1，4） B . （4，3） C . （2，4） D . （4，1）

答案解析收藏纠错 + 选题

二、填空题

11. (2021·河南模拟) (2019－π)⁰＋(－1)²⁰¹⁹＝.

答案解析收藏纠错 + 选题
12. (2023·仙桃模拟) 一个不透明的口袋中有四个完全相同的小球，其上分别标有数字1，2，4，8．随机摸取一个小球后不放回，再随机摸取一个小球，则两次取出的小球上数字之积等于8的概率是．

答案解析收藏纠错 + 选题
13. (2021·河南模拟) 关于x的方程（k﹣1）x²+2x+1＝0有两个不相等的实数根，则实数k的最大整数值为.

答案解析收藏纠错 + 选题
14. (2021·河南模拟) 如图，在扇形AOB中，∠AOB＝90°，正方形OCED的顶点C，D分别在半径OA，OB上，顶点E在 $\text{[math]}$ 上，以O为圆心，OC长为半径作 $\text{[math]}$ ，若OA＝2，则阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2021·河南模拟) 如图，在矩形ABCD中，AB＝6，BC＝12，点E在边BC上，且BE＝2CE，将矩形沿过点E的直线折叠，点C，D的对应点分别为C′，D′，折痕与边AD交于点F，当点B，C′，D′恰好在同一直线上时，AF的长为.

答案解析收藏纠错 + 选题

三、解答题

16. (2023九下·大埔期末) 先化简，再求值（ $\text{[math]}$ ﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中a，b满足a+b﹣ $\text{[math]}$ =0．

答案解析收藏纠错 + 选题
17. (2021·海东模拟) 在“优秀传统文化进校园”活动中，学校计划每周二下午第三节课时间开展此项活动，拟开展活动项目为：剪纸，武术，书法，器乐，要求七年级学生人人参加，并且每人只能参加其中一项活动．教务处在该校七年级学生中随机抽取了100名学生进行调查，并对此进行统计，绘制了如图所示的条形统计图和扇形统计图（均不完整）．
请解答下列问题：
1. （1）请补全条形统计图和扇形统计图；
2. （2）在参加“剪纸”活动项目的学生中，男生所占的百分比是多少？
3. （3）若该校七年级学生共有500人，请估计其中参加“书法”项目活动的有多少人？
4. （4）学校教务处要从这些被调查的女生中，随机抽取一人了解具体情况，那么正好抽到参加“器乐”活动项目的女生的概率是多少？
答案解析收藏纠错 + 选题
18. (2021·河南模拟) 如图，一艘游轮在海面上点O处遇到大雾，向位于A处的救援船发出求救信号，救援船指定B地为相遇地点，其中游轮在救援船的北偏西51°方向上，在相遇点B的南偏西54°方向上，相遇点B在救援船的北偏东9°方向上，救援船以50海里/时的速度行驶2小时到达B地.若游轮的速度是30海里/时，求游轮用多长时间能到达B地.(结果保留一位小数.参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73)

答案解析收藏纠错 + 选题
19. (2021·河南模拟) 如图，Rt△ABC内接于⊙O，∠BCA＝90°，∠CBA＝60°，AB＝10，点D是AB边上（异于点A，B）的一动点，DE⊥AB交⊙O于点E，交AC于点G，交切线CF于点F.
1. （1）求证：FC＝CG；
2. （2） ①当AE＝时，四边形BOEC为菱形；
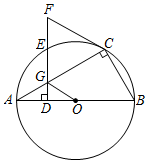
  ②当AD＝时，OG∥CF.
答案解析收藏纠错 + 选题
20. (2021·河南模拟) 如图，反比例函数y＝ $\text{[math]}$ （x＜0）的图象过格点（网格线的交点）P.
1. （1）求反比例函数的解析式；
2. （2）在图中用直尺和2B铅笔画出两个三角形（不写画法），要求每个三角形均需满足下列两个条件：
  ①三个顶点均在格点上，且其中两个顶点分别是点O，点P；
  
  ②三角形的面积等于|k|的值.
答案解析收藏纠错 + 选题
21. (2021·河南模拟) 某市中招体育测试改革，其中篮球和足球作为选考项目，某商店抓住这一商机决定购进一批篮球和足球共200个，这两种球的进价和售价如下表所示：

篮球

足球

进价（元/个）

180

150

售价（元/个）

250

200
1. （1）若商店计划销售完这批球后能获利11600元，问篮球和足球应分别购进多少个？
2. （2）设购进篮球 $\text{[math]}$ 个，获利为 $\text{[math]}$ 元，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系；
3. （3）若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元，请问有哪几种购球方案，并写出获利最大的购球方案.
答案解析收藏纠错 + 选题
22. (2021·河南模拟) 如图
1. （1）问题发现
  如图①，△ABC和△CDE均为等边三角形，直线AD和直线BE交于点F.
  
  填空：①∠AFB的度数是；
  
  ②线段AD，BE之间的数量关系为.
2. （2）类比探究
  如图②，△ABC和△CDE均为等腰直角三角形，∠ABC＝∠DEC＝90°，AB＝BC，DE＝EC，直线AD和直线BE交于点F.请判断∠AFB的度数及线段AD，BE之间的数量关系，并说明理由.
3. （3）解决问题
  如图③，在平面直角坐标系中，点A的坐标为(4，0)，点B为y轴上任意一点，连接AB，将BA绕点B逆时针旋转90°至BC，连接OC，请直接写出OC的最小值.
答案解析收藏纠错 + 选题
23. (2021·河南模拟) 如图，已知抛物线y＝﹣x²+bx+c与x轴交于A、B两点，AB＝4，交y轴于点C，对称轴是直线x＝1.
1. （1）求抛物线的解析式及点C的坐标；
2. （2）连接BC，E是线段OC上一点，E关于直线x＝1的对称点F正好落在BC上，求点F的坐标；
3. （3）动点M从点O出发，以每秒2个单位长度的速度向点B运动，过M作x轴的垂线交抛物线于点N，交线段BC于点Q.设运动时间为t（t＞0）秒.
  ①若△AOC与△BMN相似，请直接写出t的值；
  
  ②△BOQ能否为等腰三角形？若能，求出t的值；若不能，请说明理由.
答案解析收藏纠错 + 选题