山西省大同市灵丘县2019-2020学年八年级下学期数学期末...

更新时间：2024-07-13 浏览次数：140 类型：期末考试

一、单选题

1. (2024九下·秦安模拟) 下列运算正确的是（　　）

A . $\text{[math]}$ =±6 B . 4 $\text{[math]}$ ﹣3 $\text{[math]}$ =1 C . $\text{[math]}$ =6 D . $\text{[math]}$ =6

答案解析收藏纠错 + 选题
2. (2024九上·金堂月考) 以下列各组数为边长，不能构成直角三角形的是（）

A . 5，12，13 B . 1，2， $\text{[math]}$ C . 1， $\text{[math]}$ ，2 D . 4，5，6

答案解析收藏纠错 + 选题
3. (2024八下·富锦期末) 下列命题中，是真命题的是（）

A . 两条对角线互相平分的四边形是平行四边形 B . 两条对角线相等的四边形是矩形 C . 两条对角线互相垂直的四边形是菱形 D . 两条对角线互相垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
4. (2023八下·秀山期末) 如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是（）

A . 矩形 B . 菱形 C . 正方形 D . 无法判断

答案解析收藏纠错 + 选题
5. (2024八下·南乐期末) 下列函数的图象不经过第一象限，且y随x的增大而减小的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八下·宣化期末) 为了调查某校同学的体质健康状况，随机抽查了若干名同学的每天锻炼时间如表：

每天锻炼时间（分钟）

20

40

60

90

学生数

2

3

4

1

则关于这些同学的每天锻炼时间，下列说法错误的是（）

A . 众数是60 B . 平均数是21 C . 抽查了10个同学 D . 中位数是50

答案解析收藏纠错 + 选题
7. (2020八下·灵丘期末) 如图， $\text{[math]}$ 中，AC．BD为对角线，BC=3，BC边上的高为2，则阴影部分的面积为（　　）

A . 3 B . 6 C . 12 D . 24

答案解析收藏纠错 + 选题
8. (2021八下·南昌期中) 如图，在菱形ABCD中，AB＝6，∠ABC＝60°，M为AD中点，P为对角线BD上一动点，连接PA和PM，则PA＋PM的最小值是（）

A . 3 B . 2 $\text{[math]}$ C . 3 $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
9. (2022八下·宣化期末) 将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为（）．

A . 3 B . 3 $\text{[math]}$ C . 2 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022八下·宣化期末) 如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=10，点A、B的坐标分别为（2，0）、（8，0），将△ABC沿x轴向右平移，当点C落在直线y=x﹣5上时，线段BC扫过的面积为（）．

A . 80 B . 88 C . 96 D . 100

答案解析收藏纠错 + 选题

二、填空题

11. (2022八下·宣化期末) 函数y= $\text{[math]}$ 中自变量x的取值范围是

答案解析收藏纠错 + 选题
12. (2024八下·北京市期中) 有一个三角形两边长为3和4，要使该三角形为直角三角形，则第三边长为

答案解析收藏纠错 + 选题
13. (2020八下·灵丘期末) 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ ， $\text{[math]}$ 分别是函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象，则可以估计关于x的不等式 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
14. (2020八下·灵丘期末) 如图，在正方形ABCD中，点D的坐标是（0，1），点A的坐标是（-2，2），则点B的坐标为．

答案解析收藏纠错 + 选题
15. (2021八下·周村期末) 如图，点A，B，E在同一条直线上，正方形ABCD，BEFG的边长分别为3，4，H为线段DF的中点，则BH=．

答案解析收藏纠错 + 选题

三、解答题

16. (2020八下·灵丘期末) 计算：
1. （1）（ $\text{[math]}$ － $\text{[math]}$ ）× $\text{[math]}$ ．
2. （2）化简 $\text{[math]}$ ＋|a﹣1|，其中1＜a＜ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2020八下·灵丘期末) 如图，在Rt△ABC中，∠C=90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连结DE．
1. （1）证明DE∥CB；
2. （2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．
答案解析收藏纠错 + 选题
18. (2020八下·灵丘期末) 小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y（单位：千米）与时间x（单位：小时）之间函数关系的图象．根据图中提供的信息，解答下列问题：
1. （1）小帅的骑车速度为千米/小时；点C的坐标为；
2. （2）求线段AB对应的函数表达式；
3. （3）当小帅到达乙地时，小泽距乙地还有多远？
答案解析收藏纠错 + 选题

19. (2022八下·临河期末) 某班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班 50 名学生的处理方式进行统计，得出相关统计表和统计图．

组别	A	B	C	D
处理方式	迅速离开	马上救助	视情况而定	只看热闹
人数	m	30	n	5

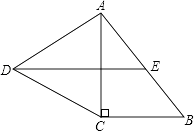
请根据表图所提供的信息回答下列问题：

（1）统计表中的 m＝，n＝；
（2）补全频数分布直方图；
（3）若该校有 2000 名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？

答案解析收藏纠错 + 选题

20. (2021八上·河源月考) 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ 的表达式为 $\text{[math]}$ ，点A ， B的坐标分别为（1，0），（0，2），直线AB与直线 $\text{[math]}$ 相交于点P ．
1. （1）求直线AB的表达式；
2. （2）求点P的坐标；
3. （3）若直线 $\text{[math]}$ 上存在一点C ，使得△APC的面积是△APO的面积的2倍，直接写出点C的坐标．
答案解析收藏纠错 + 选题
21. (2020八下·灵丘期末) 已知：如图已知直线 $\text{[math]}$ 的函数解析式为 $\text{[math]}$ ，与x轴交于点A，与y轴交于点B．
1. （1）求A、B两点的坐标；
2. （2）若点 $\text{[math]}$ 为线段 $\text{[math]}$ 上的一个动点（与A、B不重合），作 $\text{[math]}$ 轴于点E， $\text{[math]}$ 轴于点F，连接 $\text{[math]}$ ，问：
  ①若 $\text{[math]}$ 的面积为S，求S关于m的函数关系式，并写出m的取值范围；
  
  ②是否存在点P，使 $\text{[math]}$ 的值最小？若存在，求出 $\text{[math]}$ 的最小值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
22. (2020八下·灵丘期末) 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：

月销售量/件数

1770

480

220

180

120

90

人数

1

1

3

3

3

4
1. （1）直接写出这15名营业员该月销售量数据的平均数、中位数、众数；
2. （2）如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由.
答案解析收藏纠错 + 选题
23. (2020八下·灵丘期末) 在图1，2，3中，已知 $\text{[math]}$ ， $\text{[math]}$ ，点E为线段 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为边向上作菱形 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）如图1，当点E与点B重合时， $\text{[math]}$ °；
2. （2）如图2，连接 $\text{[math]}$ ．
  ①填空： $\text{[math]}$ ▲ $\text{[math]}$ （填“>”，“<”，“=”）；
  
  ②求证：点F在 $\text{[math]}$ 的平分线上；
3. （3）如图3，连接 $\text{[math]}$ ， $\text{[math]}$ ，并延长 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点H，当四边形 $\text{[math]}$ 是平行四边形时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题