河北省石家庄市2021届高三下学期数学质检试卷一

更新时间：2021-04-27 浏览次数：173 类型：高考模拟

一、单选题

1. 若集合 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足： $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 设向量 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则实数 $\text{[math]}$ （）

A . -3 B . $\text{[math]}$ C . -2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上，每人帽子的颜色互不相同，乙比戴蓝帽的人个头高，丙和戴红帽的人身高不同，戴红帽的人比甲个头小，则甲、乙、丙所戴帽子的颜色分别为（）

A . 红、黄、蓝 B . 黄、红、蓝 C . 蓝、红、黄 D . 蓝、黄、红

答案解析收藏纠错 + 选题
4. $\text{[math]}$ 是 $\text{[math]}$ 的（）

A . 充要条件 B . 必要不充分条件 C . 充分不必要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
5. 2021年是巩固脱贫攻坚成果的重要一年，某县为响应国家政策，选派了6名工作人员到 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个村调研脱贫后的产业规划，每个村至少去1人，不同的安排方式共有（）

A . 630种 B . 600种 C . 540种 D . 480种

答案解析收藏纠错 + 选题
6. 已知菱形 $\text{[math]}$ 边长为2， $\text{[math]}$ ，沿对角线 $\text{[math]}$ 折叠成三棱锥 $\text{[math]}$ ，使得二面角 $\text{[math]}$ 为60°，设 $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 为三棱锥 $\text{[math]}$ 表面上动点，且总满足 $\text{[math]}$ ，则点 $\text{[math]}$ 轨迹的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 已知数列 $\text{[math]}$ 的通项公式为 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 若 $\text{[math]}$ 图象上存在两点 $\text{[math]}$ ， $\text{[math]}$ 关于原点对称，则点对 $\text{[math]}$ 称为函数 $\text{[math]}$ 的“友情点对”（点对 $\text{[math]}$ 与 $\text{[math]}$ 视为同一个“友情点对”）若 $\text{[math]}$ 恰有两个“友情点对”，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题

9. 关于 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. 设 $\text{[math]}$ 为复数，则下列命题中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为2 D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
11. 函数 $\text{[math]}$ 的图象如图，把函数 $\text{[math]}$ 的图象上所有的点向右平移 $\text{[math]}$ 个单位长度，可得到函数 $\text{[math]}$ 的图象，下列结论正确的是（）

A . $\text{[math]}$ B . 函数 $\text{[math]}$ 的最小正周期为 $\text{[math]}$ C . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增 D . 函数 $\text{[math]}$ 关于点 $\text{[math]}$ 中心对称

答案解析收藏纠错 + 选题
12. 已知椭圆 $\text{[math]}$ 的左右焦点分别为 $\text{[math]}$ 、 $\text{[math]}$ ，长轴长为4，点 $\text{[math]}$ 在椭圆内部，点 $\text{[math]}$ 在椭圆上，则以下说法正确的是（）

A . 离心率的取值范围为 $\text{[math]}$ B . 当离心率为 $\text{[math]}$ 时， $\text{[math]}$ 的最大值为 $\text{[math]}$ C . 存在点 $\text{[math]}$ 使得 $\text{[math]}$ D . $\text{[math]}$ 的最小值为1

答案解析收藏纠错 + 选题

三、填空题

13. 已知随机变量 $\text{[math]}$ 服从正态分布 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. 如图所示，一个圆锥的侧面展开图为以 $\text{[math]}$ 为圆心，半径长为2的半圆，点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ 的长度为 $\text{[math]}$ ， $\text{[math]}$ 的长度为 $\text{[math]}$ ，则在该圆锥中，点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离为.

答案解析收藏纠错 + 选题
15. 已知定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ ，其导函数为 $\text{[math]}$ ，满足 $\text{[math]}$ ， $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集为.

答案解析收藏纠错 + 选题
16. 已知抛物线 $\text{[math]}$ 的焦点为 $\text{[math]}$ ，过 $\text{[math]}$ 且被抛物线截得的弦长为2的直线有且仅有两条，写出一个满足条件的抛物线的方程，此时该弦中点到 $\text{[math]}$ 轴的距离为.

答案解析收藏纠错 + 选题

四、解答题

17. 已知公差不为0的等差数列 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列.
（Ⅰ）求数列 $\text{[math]}$ 的通项公式；

（Ⅱ）若 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. 在 $\text{[math]}$ 中，角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所对的边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，满足 $\text{[math]}$ .
（Ⅰ）求角 $\text{[math]}$ 的大小；

（Ⅱ）若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围.

答案解析收藏纠错 + 选题
19. 2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意，沿着外墙面由低到高盘旋而成的“冰丝带”，就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹，冰上划痕成丝带，22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型，这种造型富有动感，体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体，其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就，如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式，但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理：“幂势既同，则积不容异”，才利用牟合方盖的体积推导出球的体积公式原理的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.

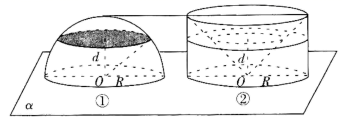
（Ⅰ）利用祖暅原理推导半径为 $\text{[math]}$ 的球的体积公式时，可以构造如图②所示的几何体 $\text{[math]}$ ，几何体 $\text{[math]}$ 的底面半径和高都为 $\text{[math]}$ ，其底面和半球体的底面同在平面 $\text{[math]}$ 内.设与平面 $\text{[math]}$ 平行且距离为 $\text{[math]}$ 的平面 $\text{[math]}$ 截两个几何体得到两个截面，请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明；

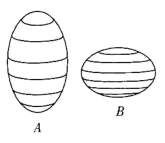
（Ⅱ）现将椭圆 $\text{[math]}$ 所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球 $\text{[math]}$ ， $\text{[math]}$ （如图），类比（Ⅰ）中的方法，探究椭球 $\text{[math]}$ 的体积公式，并写出椭球 $\text{[math]}$ ， $\text{[math]}$ 的体积之比.

答案解析收藏纠错 + 选题
20. “T2钻石联赛”是世界乒联推出一种新型乒乓球赛事，其赛制如下：采用七局四胜制，比赛过程中可能出现两种模式：“常规模式”和“FAST5模式”.在前24分钟内进行的常规模式中，每小局比赛均为11分制，率先拿满1分的选手赢得该局；如果两名球员在24分钟内都没有人赢得4局比赛，那么将进入“FAST5”模式，“FAST5”模式为5分制的小局比赛，率先拿满5分的选手赢得该局.24分钟计时后开始的所有小局均采用“FAST5”模式.某位选手率先在7局比赛中拿下4局，比赛结束.现有甲、乙两位选手进行比赛，经统计分析甲、乙之间以往比赛数据发现，24分钟内甲、乙可以完整打满2局或3局，且在11分制比赛中，每局甲获胜的概率为 $\text{[math]}$ ，乙获胜的概率为 $\text{[math]}$ ；在“FAST5”模式，每局比赛双方获胜的概率都为 $\text{[math]}$ ，每局比赛结果相互独立.
（Ⅰ）求4局比赛决出胜负的概率；

（Ⅱ）设在24分钟内，甲、乙比赛了3局，比赛结束时，甲乙总共进行的局数记为 $\text{[math]}$ ，求 $\text{[math]}$ 的分布列及数学期望.

答案解析收藏纠错 + 选题
21. 已知坐标原点为 $\text{[math]}$ ，双曲线 $\text{[math]}$ 的焦点到其渐近线的距离为 $\text{[math]}$ ，离心率为 $\text{[math]}$ .
（Ⅰ）求双曲线的方程；

（Ⅱ）设过双曲线上动点 $\text{[math]}$ 的直线 $\text{[math]}$ 分别交双曲线的两条渐近线于 $\text{[math]}$ ， $\text{[math]}$ 两点，求 $\text{[math]}$ 的外心 $\text{[math]}$ 的轨迹方程.

答案解析收藏纠错 + 选题
22. 已知函数 $\text{[math]}$ ，且方程 $\text{[math]}$ 在 $\text{[math]}$ 上有解.
（Ⅰ）求实数 $\text{[math]}$ 的取值范围；

（Ⅱ）设函数 $\text{[math]}$ 的最大值为 $\text{[math]}$ ，求函数 $\text{[math]}$ 的最小值；

答案解析收藏纠错 + 选题