 B .
B .  C .
C .  D .
D . 
抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为( )
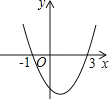
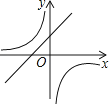 B .
B . 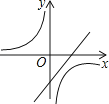 C .
C . 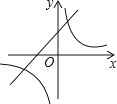 D .
D . 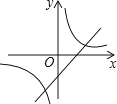




(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75).
|
组别 |
成绩 |
组中值 |
频数 |
|
第一组 |
90≤x<100 |
95 |
4 |
|
第二组 |
80≤x<90 |
85 |
m |
|
第三组 |
70≤x<80 |
75 |
n |
|
第四组 |
60≤x<70 |
65 |
21 |
根据图表信息,回答下列问题:
| 月份 | 1月 | 5月 |
| 销售量 | 3.9 万台 | 4.3 万台 |
(参考数据: ,
,
,
)