广东省佛山市禅城区2021年中考数学一模试卷

更新时间：2021-06-30 浏览次数：216 类型：中考模拟

一、单选题

1. (2020七上·清徐期末) 有理数2021的相反数为（）

A . 2021 B . -2021 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021七下·历下期中) 石墨烯是目前世界上最薄却又最坚硬同时还是导电性能最好的纳米材料，其理论厚度大约仅0.00 000 034纳米．将0.00 000 034用科学记数法表示为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·禅城模拟) 下面是“北”“比”“鼎”“射”四个字的甲骨文，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九下·香洲模拟) 下列运算中，正确的是（）

A . a⁵＋a⁵＝a¹⁰ B . 3a³•2a²＝6a⁶ C . a⁶÷a²＝a³ D . （﹣3ab）²＝9a²b²

答案解析收藏纠错 + 选题
5. (2020八上·诸城期末) 如图， $\text{[math]}$ 则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·迁西模拟) 一个小球在如图所示的地板上自由滚动，并随机停在某块方砖上．如果每一块方砖除颜色外完全相同，那么小球最终停留在黑砖上的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
7. (2021·禅城模拟) 下列一元二次方程中，没有实数根的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·禅城模拟) 点A（x₁ ， y₁），B（x₂ ， y₂）都在反比例函数y＝ $\text{[math]}$ 的图象上，且x₁＜x₂＜0，则y₁ ， y₂的大小关系是（）

A . y₂＞y₁＞0 B . y₁＞y₂＞0 C . 0＞y₂＞y₁ D . 0＞y₁＞y₂

答案解析收藏纠错 + 选题
9. (2021·禅城模拟) 下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑩个图中黑色正方形纸片的张数为（）

A . 15 B . 17 C . 21 D . 27

答案解析收藏纠错 + 选题
10. (2021·禅城模拟) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与x轴交于点 $\text{[math]}$ ，顶点坐标为 $\text{[math]}$ ，与y轴的交点在 $\text{[math]}$ ， $\text{[math]}$ 之间（包合端点），下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③关于x的方程 $\text{[math]}$ 没有实数根，其中正确结论的个数是（）

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题

二、填空题

11. (2021·禅城模拟) 计算 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2022九下·香洲模拟) 点P的坐标是 $\text{[math]}$ ，它关于y轴的对称点坐标是．

答案解析收藏纠错 + 选题
13. (2024八上·长沙月考) 若一个多边形的内角和是900º，则这个多边形是边形.

答案解析收藏纠错 + 选题
14. (2022七上·江口期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2021·禅城模拟) 如图，创新小组要测量公园内一棵树的高度AB，其中一名小组成员站在距离树10米的点E处，测得树顶A的仰角为54°.已知测角仪的架高CE＝1.5米，则这棵树的高度为米(结果保留一位小数．参考数据：sin54°≈0.8090，cos54°≈0.5878，tan54°≈1.3764)．

答案解析收藏纠错 + 选题
16. (2021·禅城模拟) 如图，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积是.

答案解析收藏纠错 + 选题
17. (2021·禅城模拟) 如图，点A、B的坐标分别为A（2，0），B（0，2），点C为坐标平面内一点，BC＝1，点M为线段AC的中点，连接OM ，则OM的最小值为．

答案解析收藏纠错 + 选题

三、解答题

18. (2021·禅城模拟) 先化简，再求值：1﹣ $\text{[math]}$ ÷ $\text{[math]}$ ，其中a＝3

答案解析收藏纠错 + 选题
19. (2022八下·霍州期末) 已知：如图，在 $\text{[math]}$ ABCD中，延长线AB至点E ，延长CD至点F ，使得BE=DF ．连接EF ，与对角线AC交于点O ．求证：OE=OF ．

答案解析收藏纠错 + 选题
20. (2021·禅城模拟) 某中学为了解全校学生参加了“交通违规”知识竞赛成绩的情况，随机抽取了一部分学生的成绩并分成四组：A组（ $\text{[math]}$ ），B组（ $\text{[math]}$ ），C组（ $\text{[math]}$ ），D组（ $\text{[math]}$ ），并绘制出如下不完整的统计图．
1. （1）求被抽取的学生成绩在C组的有多少人，并把条形统计图补充完整；
2. （2）所抽取学生的成绩的中位数落在组内；
3. （3）若该学校有1500名学生，估计这次竞赛成绩在A组的学生有多少人．
答案解析收藏纠错 + 选题
21. (2021·禅城模拟) 某农谷生态园响应国家发展有机农业政策，大力种植有机蔬菜，某超市看好甲、乙两种有机蔬菜的市场价值，经调查甲种蔬菜进价每千克 $\text{[math]}$ 元，售价每千克16元；乙种蔬菜进价每千克 $\text{[math]}$ 元，售价每千克18元．
1. （1）该超市购进甲种蔬菜10千克和乙种蔬菜5千克需要170元；购进甲种蔬菜6千克和乙种蔬菜10千克需要200元．求 $\text{[math]}$ ， $\text{[math]}$ 的值．
2. （2）该超市决定每天购进甲、乙两种蔬菜共100千克，且投入资金不少于1160元又不多于1168元，设购买甲种蔬菜 $\text{[math]}$ 千克，求有哪几种购买方案．
3. （3）在（2）的条件下，超市在获得的利润取得最大值时，决定售出的甲种蔬菜每千克捐出 $\text{[math]}$ 元，乙种蔬菜每千克捐出 $\text{[math]}$ 元给当地福利院，若要保证捐款后的利润率不低于20%，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
22. (2021·禅城模拟) 如图，反比例函数y $\text{[math]}$ 与一次函数y＝﹣x﹣（k+1）的图象在第二象限的交点为A ，在第四象限的交点为C ，直线AO（O为坐标原点）与函数y $\text{[math]}$ 的图象交于另一点B．过点A作y轴的平行线，过点B作x轴的平行线，两直线相交于点E ， △AEB的面积为6．
1. （1）求反比例函数的解析式；
2. （2）求点A ， C的坐标和△ABC的面积．
答案解析收藏纠错 + 选题
23. (2021·禅城模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的切线，A为切点，过A作 $\text{[math]}$ 的垂线 $\text{[math]}$ ，垂足为点C，交 $\text{[math]}$ 于点B．延长 $\text{[math]}$ 与 $\text{[math]}$ 交于点D，与 $\text{[math]}$ 的延长线交于点E．
1. （1）求证： $\text{[math]}$ 为 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2022九上·西安月考) 在综合与实践课上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动，如图1，将一张菱形纸片ABCD（∠BAD＞90°）沿对角线AC剪开，得到△ABC和△ACD ．
1. （1）将图1中的△ACD以A为旋转中心，逆时针方向旋转角α，使α＝∠BAC ，得到如图2所示的△AC′D ，分别延长BC和DC′交于点E ，求证四边形ACEC′是菱形；
2. （2）创新小组将图1中的△ACD以A为旋转中心，按逆时针方向旋转角α，当α与∠BAC满足什么数量关系时，得到如图3所示的四边形BCC′D是矩形，请说明理由；
3. （3）缜密小组在创样报小组发现结论的基础上，量得图3中BC＝13cm，AC＝10cm，求BD的长．
答案解析收藏纠错 + 选题
25. (2021·禅城模拟) 综合与探究
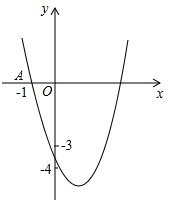
如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ，过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E．连接PD，与BC交于点F．设点P的运动时间为t秒（t>0）．
1. （1）求直线BC的函数表达式．
2. （2） ①直接写出P、D两点的坐标（用含t的代数式表示，结果需化简）．
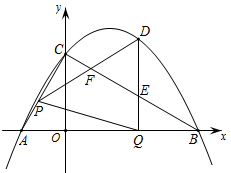
  ②在点P、Q运动的过程中，当PQ=PD时，求t的值．
3. （3）试探究在点P、Q运动的过程中，是否存在某一时刻，使得点F为PD的中点．若存在，请直接写出此时t的值与点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题