浙江省宁波市余姚市2020-2021学年阳明杯竞赛七年级下学...

更新时间：2021-06-24 浏览次数：351 类型：竞赛测试

一、选择题（每小题4分，共32分。）

1. (2021七下·余姚竞赛) 下列是二元一次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . x=y²+1 D . x+y=1

答案解析收藏纠错 + 选题
2. (2021七下·余姚竞赛) 下列计算结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021七下·余姚竞赛) 下列调查中，需要采用全面调查方式的是（）

A . 对某批次汽车的抗撞击能力的调查 B . 为防控新冠肺炎，对高风险地区人员进行核酸检测 C . 对全国中学生课外阅读情况的调查 D . 对某一批次盒装牛奶的合格情况的调查

答案解析收藏纠错 + 选题
4. (2021七下·余姚竞赛) 如图，能判定DE∥BC的条件是（）

A . ∠ABC+∠BAE=180 B . ∠C=∠BAC C . ∠C+∠BAD=180 D . ∠C=∠BAD

答案解析收藏纠错 + 选题
5. (2021七下·余姚竞赛) 下列分解因式正确的是（）

A . a²－4=（a－2）² B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021七下·余姚竞赛) 如图，在框中解分式方程的4个步骤中，根据等式基本性质的是（）

A . ①③ B . ②④ C . ①② D . ③④

答案解析收藏纠错 + 选题
7. (2021七下·余姚竞赛) 对于分式 $\text{[math]}$ ，当 $\text{[math]}$ 时，下列结论正确的是（）

A . 分式无意义 B . 分式值为0 C . 当 $\text{[math]}$ 时，分式的值为0 D . 当 $\text{[math]}$ 时，分式的值为0

答案解析收藏纠错 + 选题
8. (2021七下·余姚竞赛) 已知 $\text{[math]}$ 加上一个单项式后能成为一个整式的完全平方，给出下面四个单项式① $\text{[math]}$ ， ② $\text{[math]}$ ， ③ $\text{[math]}$ 1 ， ④ $\text{[math]}$ ，其中满足条件的共有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题（每小题5分，共30分）

9. (2021七下·余姚竞赛) 石墨烯是目前世界上最薄、最坚硬的纳米材料，厚度仅0.000 0034m，用科学记数法表示0.000 0034=．

答案解析收藏纠错 + 选题
10. (2021七下·余姚竞赛) 已知a﹣b＝3，ab＝﹣2，则a²b﹣ab²的值为．

答案解析收藏纠错 + 选题
11. (2021七下·余姚竞赛) 若多项式x²+m x+n可以因式分解为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2021七下·余姚竞赛) 七年级（1）班一次数学单元测试，全班所有学生成绩的频数直方图如图所示（满分100分，成绩取整数），则成绩在90.5～95.5这一分数段的频率是．

答案解析收藏纠错 + 选题
13. (2021七下·余姚竞赛) 将一把直尺和一块直角三角板如图放置，如果∠α=43°，则∠β的度数是度．

答案解析收藏纠错 + 选题
14. (2021七下·余姚竞赛) 在“幻方拓展课程”探索中，小明在如图的3×3方格内填入了一些表示数的代数式，若图中各行、各列及对角线上的三个数之和都相等，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题（共58分）

15. (2021七下·余姚竞赛) 计算下列各题
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$
答案解析收藏纠错 + 选题
16. (2021七下·余姚竞赛) 解方程（组）
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2021七下·余姚竞赛) 如图，已知∠1=∠2，∠B=∠C ，可推得AB∥CD ．理由如下：
∵∠1=∠2（已知），

又∠1=∠CGD（        ）

∴∠2=∠CGD

∴CE∥BF（        ）

∴∠_▲_=∠BFD（        ）

又∵∠B=∠C（已知）

∴__▲__

∴AB∥CD（        ）

答案解析收藏纠错 + 选题
18. (2021七下·余姚竞赛) 如图，正方形网格中有一个△ABC（其中A，B，C均在格点上），按要求进行下列作图（只借助于网格，需标上字母写出结论）

（ 1 ）过点A画出BC的平行线；

（ 2 ）画出先将△ABC向右平移5格，再向上平移3格后的△DEF；

答案解析收藏纠错 + 选题
19. (2021七下·余姚竞赛) 为提高学生的音乐素养，培养学生的音乐兴趣，某校举行了一次“听音辨曲”活动．随机抽取了部分学生进行测试，并将测试成绩从高到低分为A（优秀），B（良好），C（合格），D（不合格）四个等级，制作了如下的统计图（扇形统计图中，等级“C”所对应的扇形的圆心角为90度，部分信息不完整）：

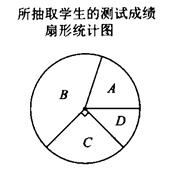
根据上述统计图，完成以下问题：
1. （1）这次共抽取了名学生；在扇形统计图中，等级“D”所对应的扇形的圆心角是度．
2. （2）请把条形统计图补充完整．
3. （3）已知该校共有1800名学生参加测试，请你估算该校获得等级“A”的学生人数．
答案解析收藏纠错 + 选题
20. (2021七下·余姚竞赛) 材料阅读：若一个整数能表示成a²+b²（a、b是正整数）的形式，则称这个数为“完美数”．例如：因为13=3²+2² ，所以13是“完美数”；再如：因为a²+2ab+2b²=（a+b）²+b²（a、b是正整数），所以a²+2ab+2b²也是“完美数”．
1. （1）解决问题：
  请你写出一个大于20小于30 的“完美数”，并判断53是否为“完美数”；
2. （2）探究问题：
  ①已知x²+y²-2x+4y+5＝0，求x+y的值．
  
  ②已知S＝x²+4y²+4x-12y+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．
答案解析收藏纠错 + 选题

四、附加选择题（每小题4分，共8分）

21. (2021七下·余姚竞赛) 已知 $\text{[math]}$ （ $\text{[math]}$ 为任意有理数），则M与N的大小关系是（）

A . M>N B . M<N C . M ≥N D . M ≤ N

答案解析收藏纠错 + 选题
22. (2021七下·余姚竞赛) 如图，大长方形ABCD是由一张周长为C₁正方形纸片①和四张周长分别为C₂ ， C₃ ， C₄ ， C₅的长方形纸片②，③，④，⑤拼成，若大长方形周长为定值，则下列各式中为定值的是（）

A . C₁ B . C₃+C₅ C . C₁+C₃+C₅ D . C₁+C₂+C₄

答案解析收藏纠错 + 选题

五、附加填空题（每小题5分，共10分）

23. (2021七下·余姚竞赛) 如果关于x的分式方程 $\text{[math]}$ 有增根，则m的值为．

答案解析收藏纠错 + 选题
24. (2021七下·余姚竞赛) a ， b是实数，定义关于“*”的一种运算：a*b＝ $\text{[math]}$ ．则下列结论：
①a*b＝0，则a＝0或b＝0； ②不存在实数a ， b ，满足a*b＝4a²+b²；

③a*（b+c）＝a*b+a*c； ④a*b＝8，则（10ab³）÷（5b²）＝4 ，

其中正确的结论是．（用序号表示出所有正确的结论）

答案解析收藏纠错 + 选题

六、附加解答题

25. (2021七下·余姚竞赛) 一张如图1的长方形铁皮，四个角都剪去边长为 30 厘米的正方形，再四周折起，做成一个有底无盖的铁盒如图2．
1. （1）现有一批图1规格的铁皮需甲、乙两队加工，已知甲队加工300张铁皮与乙队加工360张铁皮所用时间相同. 若乙队每天比甲队多加工30张，求甲队每天加工铁皮的张数.
2. （2）已知铁盒底面长方形的长是 $\text{[math]}$ cm，宽是 $\text{[math]}$ cm，这个无盖铁盒各个面的面积之和称为铁盒的全面积．
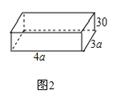
  ①若要在铁盒的各个外表面漆上某种油漆，每元钱可漆的面积为 $\text{[math]}$ （cm²），则油漆这个铁盒需要多少钱（用含 $\text{[math]}$ 的代数式表示）？
  
  ②是否存在一个正整数 $\text{[math]}$ ，使得铁盒的全面积是底面积的正整数倍？若存在，请求出所有 $\text{[math]}$ ，若不存在，请说明理由．
答案解析收藏纠错 + 选题