重庆市2021年初中学业水平暨高中招生考试数学模拟卷一

更新时间：2021-07-10 浏览次数：312 类型：中考模拟

一、单选题

1. (2021·重庆模拟) 下列各数中，最大的数是（）

A . $\text{[math]}$ B . 0 C . 2 D . 4

答案解析收藏纠错 + 选题
2. (2021·重庆模拟) 下列汽车标志中，既是中心对称图形，又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021·重庆模拟) 据报道，2020年重庆中考参考人数为34.97万人，普通高中招生人数为21.3万人，普通高中录取率为60%，竞争压力巨大.其中数据“21.3万”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·重庆模拟) 把黑色小圆圈按照如图所示的规律拼图案，其中第①个图案有3个黑色小圆圈，第②个图案有8个黑色小圆圈，第③个图案有15个黑色小圆圈，…，按照规律排下去，则第⑥个图案中黑色小圆圈的个数是（）

A . 35 B . 48 C . 63 D . 67

答案解析收藏纠错 + 选题
5. (2021·重庆模拟) 如图， $\text{[math]}$ 是等腰三角形，且 $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，与 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·重庆模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·重庆模拟) 解一元一次方程 $\text{[math]}$ 时，去分母正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·重庆模拟) 如图，在平面直角坐标系中， $\text{[math]}$ 的顶点坐标分别是 $\text{[math]}$ ，以点 $\text{[math]}$ 为位似中心，在点 $\text{[math]}$ 异侧作 $\text{[math]}$ ，使得 $\text{[math]}$ 与 $\text{[math]}$ 成位似图形，且位似比为 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·重庆模拟) 位于重庆西部的融创文旅城是集商场、室内乐园、室外飞天项目、渝乐小镇于一体的大型文娱项目，小明为了测量室外飞天项目中摩天轮最高处点 $\text{[math]}$ 距离地面 $\text{[math]}$ 的高度 $\text{[math]}$ ，他先是在 $\text{[math]}$ 处测得顶点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，然后沿水平向摩天轮方向前行了50米到达 $\text{[math]}$ 处，再沿着坡比为 $\text{[math]}$ 的小山坡走到点 $\text{[math]}$ ，测得 $\text{[math]}$ 米，此时点 $\text{[math]}$ 到 $\text{[math]}$ 的水平距离为70米， $\text{[math]}$ 与地面 $\text{[math]}$ 垂直，则摩天轮最高处点 $\text{[math]}$ 距离地面 $\text{[math]}$ 的高度 $\text{[math]}$ 约为（参考数据： $\text{[math]}$ ）（）米

A . 90.2 B . 91.3 C . 93.4 D . 95.42

答案解析收藏纠错 + 选题
10. (2021·重庆模拟) 关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 有且仅有三个整数解，且关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 有整数解，则符合条件的整数 $\text{[math]}$ 的个数为（）

A . 3 B . 2 C . 1 D . 0

答案解析收藏纠错 + 选题
11. (2021·重庆模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ .若 $\text{[math]}$ ，则点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021·重庆模拟) 如图，在平面直角坐标系中， $\text{[math]}$ 斜边 $\text{[math]}$ 中点与原点 $\text{[math]}$ 重合， $\text{[math]}$ 点是平面内第二象限内一点，且 $\text{[math]}$ 平分 $\text{[math]}$ ，连接 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 两点.已知 $\text{[math]}$ 两点横坐标分别为 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . -4 C . $\text{[math]}$ D . -2

答案解析收藏纠错 + 选题

二、填空题

13. (2021·重庆模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2021·重庆模拟) 一个正多边形的内角度数为 $\text{[math]}$ ，则这个正多边形的边数为.

答案解析收藏纠错 + 选题
15. (2021·重庆模拟) 在一个不透明的纸箱内装有形状、质地、大小、颜色完全相同的5张卡片，卡片上分别标有数字-3，-1，0，1，2，将它们洗匀后，背面朝上，从中随机抽取1张，把抽得的数字记作 $\text{[math]}$ ，再从剩下的卡片中随机抽取1张，把抽得的数字记作 $\text{[math]}$ ，则使得反比例函数 $\text{[math]}$ 的图象经过第一、三象限的概率为.

答案解析收藏纠错 + 选题
16. (2021·重庆模拟) 如图，正方形 $\text{[math]}$ 中，分别以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画圆弧，两弧交于点 $\text{[math]}$ .若正方形的边长为3，则图中阴影部分面积为.（结果保留 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
17. (2021·重庆模拟) 小亮和小颖两位同学从距离图书馆3000米的同一小区同时出发，各自去还图书，然后再从图书馆借书后原路原速返回自己居住的小区（借书、还书等逗留时间忽略不计），在整个过程中，两位同学的速度均保持匀速行驶，且小亮的速度快于小颖，两人相距的路程 $\text{[math]}$ （米）与小亮离开小区的时间 $\text{[math]}$ （分）之间的关系如图中折线所示，则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
18. (2021·重庆模拟) 为了迎接中秋佳节，沁园在9月30日以及10月1日两天对“阖家悦”“吉如意”“福满圆”三种型号的月饼进行降价促销.经计算，结果发现10月1日“阖家悦”“吉如意”“福满圆”三种月饼销量分别在9月30日的基础上减少了30%，64%，40%，且这三种月饼的总销量是9月30日的 $\text{[math]}$ ，10月1日“阖家悦”“福满圆”两种型号月饼的销量之和是9月30日“阖家悦”“福满圆”两种型号月饼的销量之和的 $\text{[math]}$ ，那么10月1日“吉如意”月饼的销量与这两天的总销量之比为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021·重庆模拟) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题

20. (2021·重庆模拟) 为了了解学生对2022年北京冬奥会相关信息的情况，某校学生发展中心举行了以“纯洁的冰雪，激情的约会”为主题的知识测试活动.现从该校八，九年级中各随机抽取了15名学生的测试成绩（百分制）进行整理、描述和分析（成绩得分用 $\text{[math]}$ 表示，共分成四组：A. $\text{[math]}$ ，B. $\text{[math]}$ ，C. $\text{[math]}$ ，D. $\text{[math]}$ ），下面给出了部分信息八年级15名学生的竞赛成绩是：99，80，99，86，99，96，90，100，88，87，87，89，86，95，99

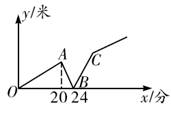
九年级15名学生的竞赛成绩在 $\text{[math]}$ 组中的数据是：94，90，94.

八，九年级抽取学生的测试成绩统计表

年级	平均数	中位数	众数	90分及以上人数所占百分比
八年级	92	90	$\text{[math]}$	53.3%
九年级	92	$\text{[math]}$	100	$\text{[math]}$

九年级抽取学生的测试成绩扇形统计图

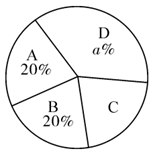
根据以上信息，解答下列问题：

（1）直接写出上述图表中 $\text{[math]}$ 的值： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
（2）由以上数据，你认为该校八、九年级中哪个年级学生掌握2022年北京冬奥会知识较好？请说明理由（一条理由即可）
（3）该校八、九年级共2700人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀 $\text{[math]}$ 的学生人数是多少？

答案解析收藏纠错 + 选题

21. (2021·重庆模拟) 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 中点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ .
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题

22. (2021·重庆模拟) 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程.以下是我们研究函数 $\text{[math]}$ 的性质及其应用的部分过程，请按要求完成下列各小题.

（1）该函数的自变量取值范围是；

（2）根据下表的条件，求出 $\text{[math]}$ 的值： $\text{[math]}$ ， $\text{[math]}$ ；

$\text{[math]}$

…

-5

-4

-3

-2

-1

…

$\text{[math]}$

…

$\text{[math]}$

…

（3）根据平面直角坐标系中点的位置，补全函数图象；
（4）根据所补全的函数图象，判断下列关于该函数性质的说法是否正确；
①该函数图象是中心对称图形，它的对称中心为原点；（）

②该函数在自变量的取值范围内，有最小值，当 $\text{[math]}$ 时，函数取得最小值 $\text{[math]}$ ；（）

③当 $\text{[math]}$ 或 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大；当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小；（）
（5）若不等式 $\text{[math]}$ ，结合函数图象，直接写出 $\text{[math]}$ 的取值范围.（保留1位小数，误差不超过0.2）

答案解析收藏纠错 + 选题

23. (2021·重庆模拟) 对任意非零的三位数 $\text{[math]}$ ，如果其个位上的数字与十位上的数字之和等于百位上的数字，则称 $\text{[math]}$ 为“巧合数”，现将 $\text{[math]}$ 的个位数作为百位数，百位数作为十位数，十位数作为个位数，得到一个新数 $\text{[math]}$ ，并规定 $\text{[math]}$ .例如532是一个“巧合数”，个位数作为百位数，百位数作为十位数，十位数作为个位数，得到一个新数 $\text{[math]}$ ，所以 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ 除以8恰好余4，则称 $\text{[math]}$ 是“十分巧合数”，求出所有的“十分巧合数”.
答案解析收藏纠错 + 选题
24. (2021·重庆模拟) 夏季是葡萄上市的季节，某超市7月购进巨玫瑰和金手指两个品种的葡萄进行销售.已知巨玫瑰葡萄的售价为40元/千克，金手指葡萄的售价为50元/千克，统计发现，第一周共卖岀两个品种的葡萄800千克.
1. （1）若卖出巨玫瑰葡萄的总销售额不低于金手指葡萄的 $\text{[math]}$ ，求至少卖岀巨玫瑰葡萄多少千克；
2. （2）由于7月份第二周葡萄大量上市，该店决定对两ˆ品种的葡萄进行降价销售.巨玫瑰葡萄降价 $\text{[math]}$ ，金手指葡萄降价 $\text{[math]}$ ，结果巨玫瑰葡萄的销量在（1）中的最小销量下增加 $\text{[math]}$ ，而金手指葡萄的销量在（1）中最高销量基础上增加了 $\text{[math]}$ ，最终7月份第二周的总销售额为36000元，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
25. (2021·重庆模拟) 如图，抛物线 $\text{[math]}$ 交于 $\text{[math]}$ 轴于 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），且 $\text{[math]}$ 两点的横坐标分别是 $\text{[math]}$ 和2，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，且 $\text{[math]}$ 的面积为24.
1. （1）求抛物线的解析式.
2. （2）如图1，若 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，点 $\text{[math]}$ 是抛物线上 $\text{[math]}$ 下方的一动点，连接 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最大值以及最大值时点 $\text{[math]}$ 的坐标.
3. （3）如图2，将原抛物线向右平移4个单位长度，得到新的抛物线 $\text{[math]}$ ，平移后的抛物线与原抛物线的交点为 $\text{[math]}$ .在（2）的条件下，在直线 $\text{[math]}$ 上是否存在一点 $\text{[math]}$ ，在平面直角坐标系中是否存在一点 $\text{[math]}$ ，使得以 $\text{[math]}$ 为顶点的四边形是菱形？若存在，直接写出点 $\text{[math]}$ 的坐标，若不存在，说明理由.
答案解析收藏纠错 + 选题
26. (2021·重庆模拟) 在等腰直角 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转一定的角度得到线段 $\text{[math]}$ .连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作线段 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）如图1，若 $\text{[math]}$ .
  ①求 $\text{[math]}$ 的度数；
  
  ②连接 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）如图2，若 $\text{[math]}$ ，当 $\text{[math]}$ 时，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题