安徽省2021年中考数学试卷

更新时间：2021-07-06 浏览次数：627 类型：中考真卷

一、选择题（本大题共10小题，每小题4分，满分40分）

1. (2021·安徽) ﹣9的绝对值是（）

A . 9 B . ﹣9 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七下·蒙城月考) 《2020年国民经济和社会发展统计公报》显示，2020年我国共资助8990万人参加基本医疗保险，其中8990万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·安徽) 计算 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·包头模拟) 几何体的三视图如图所示，这个几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·安徽) 两个直角三角板如图摆放，其中∠BAC=∠EDF=90°，∠E=45°，∠C=30°，AB与DF交于点M，若BC∥EF，则∠BMD的大小为（）

A . 60° B . 67.5° C . 75° D . 82.5°

答案解析收藏纠错 + 选题
6. 某品牌鞋子的长度y cm与鞋子的“码”数x之间满足一次函数关系，若22码鞋子的长度为16 cm，44码鞋子的长度为27 cm。则38码鞋子的长度为（）

A . 23 cm B . 24 cm C . 25 cm D . 26 cm

答案解析收藏纠错 + 选题
7. (2024七下·方城期中) 设 $\text{[math]}$ 为互不相等的实数，且 $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·寻乌模拟) 如图，在菱形ABCD中，AB=2，∠A=120°，过菱形ABCD的对称中心O分别作边AB，BC的垂线，交各边于点E，F，G，H.则四边形EFGH的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·安徽) 如图，在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点A的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·安徽) 在△ABC中∠ACB=90°，分别过点B，C作∠BAC平分线的垂线，垂足分别为点D，E，BC的中点是M，连接CD，MD，ME.则下列结论错误的是（）

A . CD=2ME B . ME∥AB C . BD=CD D . ME=MD

答案解析收藏纠错 + 选题

二、填空题（本大题共4小题，每小题5分，满分20分）

11. (2021·安徽) 计算 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022八上·泗县期中) 埃及胡夫金字塔是古代世界建筑奇迹之一，其底面是正方形，侧面是全等的等腰三角形，底面正方形的边长与侧面等腰三角形底边上的高的比值是 $\text{[math]}$ ，它介于整数n和n+1之间，则n的值是.

答案解析收藏纠错 + 选题
13. (2021·安徽) 如图，圆O的半径为1，△ABC内接于圆O，若∠A=60°，∠B=75°，则AB=.

答案解析收藏纠错 + 选题
14. (2021·安徽) 设抛物线 $\text{[math]}$ ，其中 $\text{[math]}$ 为实数.
1. （1）若抛物线经过点 $\text{[math]}$ ，则 $\text{[math]}$ .
2. （2）将抛物线 $\text{[math]}$ 向上平移2个单位，所得抛物线顶点的纵坐标的最大值是.
答案解析收藏纠错 + 选题

三、（本大题2个小题，每小题8分，共16分）

15. (2021·安徽) 解不等式： $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2021·安徽) 如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点（网格线的交点）上.

⑴将△ABC向右平移5个单位得到△ $\text{[math]}$ ；

⑵将(1)中的△ $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转90°得到△ $\text{[math]}$ ，画出△ $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、（本大题2个小题，每小题8分，共16分）

17. (2021·安徽) 学生到工厂劳动实践，学习机械零件，零件的截面如图所示，已知四边形AEFD为矩形，点B，C分别在EF，DF上，∠ABC为90°，∠BAD＝53°，AB＝10cm，BC=6cm，求零件的截面面积.
参考数据：sin53°≈0.80，cos53°≈0.60.

答案解析收藏纠错 + 选题
18. (2021·安徽) 某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成，图1表示此人行道的地砖排列方式，其中正方形地砖为连续排列.
【观察思考】

当正方形地砖只有1块时，等腰直角三角形地砖有6块(如图2)；当正方形地砖只有2块时，等腰直角三角形地砖有8块(如图2)；以此类推.

【规律总结】
1. （1）若人行道上每增加一块正方形地砖，则等腰直角三角形地砖增加块；
2. （2）若一条这样的人行道一共有n(n为正整数)块正方形地砖，则等腰直角三角形地砖的块数为(用含n的代数式表示).
3. （3）【问题解决】
  现有2021块等腰直角三角形地砖，若按此规律再建一条人行道，要求等腰直角三角形地砖剩余最少，则需要正方形地砖多少块？
答案解析收藏纠错 + 选题

五、（本大题2个小题，每小题10分，共20分）

19. (2021·安徽) 已知正比例函数y=kx(k≠0)与反比例函数 $\text{[math]}$ 的图像都经过点A(m，2).
1. （1）求k，m的值；
2. （2）在图中画出正比例函数y=kx的图像，并根据图像，写出正比例函数值大于反比例函数值时x的取值范围.
答案解析收藏纠错 + 选题
20. (2021·安徽) 如图，圆O中两条互相垂直的弦AB，CD交于点E.
1. （1） M是CD的中点，OM等于3，CD=12，求圆O的半径长；
2. （2）点F在CD上，且CE=EF，求证：AF⊥BD.
答案解析收藏纠错 + 选题

六、（本题满分12分）

21. (2021·安徽) 为了解全市居民用户用电情况，某部门从居民用户中随机抽取100户进行月用电量(单位：kM·h)调查，按月用电量50～100，100～150，100～200，200～250，250～300，300～350进行分组，绘制频数分布直方图如下：

（1）求频数分布直方图中x的值；
（2）判断这100户居民用户月用电量数据的中位数在哪一组(直接写出结果)；

（3）设各组居民月平均用电量如下表：

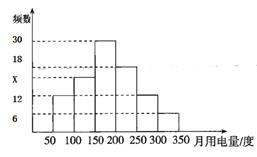
组别	50～100	100～150	150～200	200～250	250～300	300～350
月平均用电量（单位：kM·h）	75	125	175	225	275	325

根据上述信息，估计该市居民用户月用电量的平均数.

答案解析收藏纠错 + 选题

七、（本题满分12分）

22. (2021·安徽) 已知抛物线 $\text{[math]}$ 的对称轴为直线x=1.
1. （1）求a的值；
2. （2）若点M( $\text{[math]}$ , $\text{[math]}$ ),N( $\text{[math]}$ , $\text{[math]}$ )都在此抛物线上，且-1＜ $\text{[math]}$ ＜0，1＜ $\text{[math]}$ ＜2.比较 $\text{[math]}$ 和 $\text{[math]}$ 的大小，并说明理由；
3. （3）设直线y=m(m＞0)与抛物线 $\text{[math]}$ 交于A、B，与抛物线 $\text{[math]}$ 交于C、D，求线段AB与线段CD的长度之比.
答案解析收藏纠错 + 选题

八、（本题满分14分）

23. (2021·安徽) 如图1，在四边形ABCD中，∠ABC=∠BCD，点E在边BC上，且AE∥CD，DE∥AB，CF∥AD交线段AE于点F，连接BF.
1. （1）求证：△ABF≌△EAD；
2. （2）如图2，若AB=9，CD=5，∠ECF＝∠AED，求BE的长；
3. （3）如图3，若BF的延长线经过AD的中点M，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

安徽省2021年中考数学试卷

副标题：

*注意事项：

安徽省2021年中考数学试卷

试题分析

总体分析

题量分析

难度分析

知识点分析