 B .
B .  C .
C .  D .
D . 
| 文化程度 | 高中 | 大专 | 本科 | 硕士 | 博士 |
| 人数 | 9 | 17 | 20 | 9 | 5 |
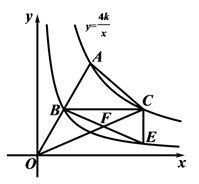

|
类别 |
A |
B |
C |
D |
E |
F |
|
类型 |
足球 |
羽毛球 |
乒乓球 |
篮球 |
排球 |
其他 |
|
人数 |
10 |
4 |
6 |
2 |
根据以上信息,解答下列问题:


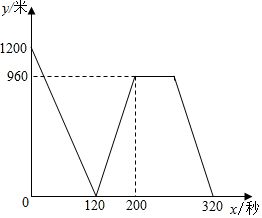

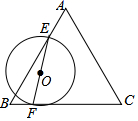
①直接写出 的度数;
②当 时,求点F的坐标;并探索
是否有最大值?如果有,请求出;如果没有,请说明理由.
②求y关于x的函数表达式及自变量x的取值范围.