浙江省台州市仙居县2020-2021学年七年级下学期期末数学...

更新时间：2024-07-13 浏览次数：277 类型：期末考试

一、选择题（本大题有10小题，每小题3分，共30分。）

1. (2021八上·长安期中) 下列实数中，为无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 5 D . π

答案解析收藏纠错 + 选题
2. (2021七下·仙居期末) 下列采用的调查方式中，不合适的是（）

A . 了解永安溪的水质，采用抽样调查 B . 检测神舟十二号飞船的零部件质量，采用抽样调查 C . 了解我县中学生视力情况，采用抽样调查 D . 了解某班同学的数学成绩，采用全面调查

答案解析收藏纠错 + 选题
3. (2021七下·仙居期末) $\text{[math]}$ ﹣1介于下列哪两个整数之间（）

A . ﹣1与0 B . 0与1 C . 1与2 D . 2与3

答案解析收藏纠错 + 选题
4. (2022七下·高邑期中) 已知二元一次方程4x+5y＝5，用含x的代数式表示y ，则可表示为（）

A . y＝﹣ $\text{[math]}$ x+1 B . y＝﹣ $\text{[math]}$ x﹣1 C . y＝ $\text{[math]}$ x+1 D . y＝ $\text{[math]}$ x﹣1

答案解析收藏纠错 + 选题
5. (2022七下·梁园期末) 已知a＞b ，则下列不等式成立的是（）

A . a+3＞b+4 B . 2a＜2b C . a﹣1＞b﹣1 D . ﹣4a＞﹣4b

答案解析收藏纠错 + 选题
6. (2022七下·临海开学考) 如图，直线AB ， CD相交于点O ， OA平分∠EOC ．若∠BOD＝42°，则∠EOD的度数为（）

A . 96° B . 94° C . 104° D . 106°

答案解析收藏纠错 + 选题
7. (2023七下·腾冲期末) 已知x ， y满足方程组 $\text{[math]}$ ，则x+3y的值为（）

A . 3 B . $\text{[math]}$ C . 5 D . 6

答案解析收藏纠错 + 选题
8. (2021七下·仙居期末) 小敏妈妈为小敏爸爸购买了一双运动鞋．小敏、哥哥和爸爸都想知道这双鞋的价格，妈妈让他们猜．爸爸说“至少300元．”哥哥说：“至多260元．”小敏说：“至多200元．”妈妈说：“你们三个人都说错了．”则这双鞋的价格x（元）所在的范围是（）

A . 200＜x＜260 B . 260＜x＜300 C . 200≤x≤260 D . 260≤x≤300

答案解析收藏纠错 + 选题
9. (2022七下·北仑期中) 在螳螂的示意图中，AB∥DE ， ∠ABC＝126°，∠CDE＝70°，则∠BCD＝（）

A . 14° B . 16° C . 18° D . 20°

答案解析收藏纠错 + 选题
10. (2021七下·仙居期末) 计算机的某种运算程序如图：

已知输入3时输出的运算结果是5，输入4时输出的运算结果是7．若输入的数是x（x≠0）时输出的运算结果为P ，输入的数是3x时输出的运算结果为Q ，则（）

A . P：Q＝3 B . Q：P＝3 C . （Q﹣1）：（P﹣1）＝3 D . （Q+1）：（P+1）＝3

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题3分，共18分）

11. (2021七下·仙居期末) 如图，三角形ABC中，AC⊥BC ，则边AC与边AB的大小关系是，依据是．

答案解析收藏纠错 + 选题
12. (2021七下·仙居期末) 在平面直角坐标系中，若点A（2m，m+3）在第三象限，则m的取值范围是．

答案解析收藏纠错 + 选题
13. (2021七下·仙居期末) 某班用700元钱购买足球和篮球共11个，其中篮球单价为50元/个，足球单价为80元/个，若设购买篮球x个，足球y个，则可列方程组为．

答案解析收藏纠错 + 选题
14. (2021七下·仙居期末) 关于x的不等式组 $\text{[math]}$ 的解集为﹣1＜x＜2，则a+b的值为．

答案解析收藏纠错 + 选题
15. (2022七下·梁园期末) 如图，在平面直角坐标系中，将正方形①依次平移后得到正方形②，③，④…；相应地，顶点A依次平移得到A₁ ， A₂ ， A₃ ， …，其中A点坐标为（1，0），A₁坐标为（0，1），则A₂₀的坐标为．

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，17题4分，18～21题每题6分，22～24题每题8分，共52分）

16. (2021七下·仙居期末) 计算：|﹣ $\text{[math]}$ |﹣ $\text{[math]}$ + $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2021七下·仙居期末) 解不等式 $\text{[math]}$ ＜ $\text{[math]}$ ，并把它的解集在数轴上表示出来．

答案解析收藏纠错 + 选题

18. (2021七下·仙居期末) 小明同学解方程组 $\text{[math]}$ 的过程如下：

解：①×2，得2x﹣6y＝2③

③﹣②，得﹣6y﹣y＝2﹣7

﹣7y＝﹣5，y＝ $\text{[math]}$ ；

把y＝ $\text{[math]}$ 代入①，得x﹣3× $\text{[math]}$ ＝1，x＝ $\text{[math]}$

所以这个方程组的解是 $\text{[math]}$

你认为他的解法是否正确？若正确，请写出每一步的依据；若错误，请写出正确的解题过程．

答案解析收藏纠错 + 选题

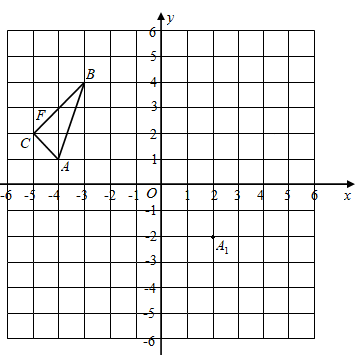
19. (2021七下·仙居期末) 如图，在方格纸中，三角形ABC的三个顶点均为格点，当三角形ABC平移后，得到三角形A₁B₁C₁ ，其中点A与A₁（2，﹣2），点B与B₁ ，点C与C₁对应．
1. （1）画出三角形A₁B₁C₁ ，并写出点B₁ ， C₁的坐标；
2. （2） F（a ， b）是边BC上一点，请写出点F的对应点F₁的坐标．
答案解析收藏纠错 + 选题
20. (2021七下·仙居期末) 已知：如图，三角形ABC中，AC⊥BC ． F是边AC上的点，连接BF ，作EF∥BC且交AB于点E ．过点E作DE⊥EF ，交BF于点D ．

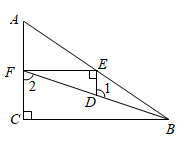
求证：∠1+∠2＝180°．

下面是证明过程，请在横线上填上适当的推理结论或推理依据．

证明：

∵AC⊥BC（已知），

∴∠ACB＝90°（垂直的定义）．

∵EF∥BC（已知），

∴∠AFE＝▲ ＝90°（ ▲）．

∵DE⊥EF（已知），

∴∠DEF＝90°（垂直的定义）．

∴∠AFE＝∠DEF（等量代换），

∴▲∥▲（ ▲）．

∴∠2＝∠EDF（ ▲）．

又∵∠EDF+∠1＝180°（邻补角互补），

∴∠1+∠2＝180°（等量代换）．

答案解析收藏纠错 + 选题
21. (2021七下·仙居期末) 近年来，随着人们健康睡眠的意识不断提高，社会各界对于初中生的睡眠时间是否充足越发关注，近日某学校从全校1600人中随机抽取了部分同学，调查他们平均每日睡眠时间，将得到的数据整理后绘制了如图所示的不完整的扇形统计图和频数分布直方图：
1. （1）本次接受调查的人数为；
2. （2）补全直方图；
3. （3）教育部《关于进一步加强中小学生睡眠管理工作的通知》文件指出，初中生睡眠时间应达到9小时，试估计该校学生睡眠时间达标人数，并评价该校初中生睡眠时间情况．
答案解析收藏纠错 + 选题
22. (2021七下·仙居期末) 已知：在三角形ABC和三角形DEF中，AB∥DE ．
1. （1）如图1，若三角形DEF的顶点F在三角形ABC的边AB上，且DF∥AC ．
  求证：∠A＝∠D；
2. （2）如图2，若三角形DEF的顶点F在三角形ABC的内部，∠A＝∠D ，则DF与AC有怎样的位置关系？请说明理由．
答案解析收藏纠错 + 选题
23. (2021七下·仙居期末) 某杨梅经销商以每千克40元的价格分三批向果农购进杨梅，均分拣成“特优”和“普通”两类销售，分拣和包装费用为每千克6元．每批杨梅中最差的10%不能销售，为损耗，其余杨梅均能售完．“特优”杨梅售价是每千克110元，“普通”杨梅售价为每千克30元．
1. （1）该经销商购进的第一批杨梅为500千克，分拣出“特优”杨梅150千克，则他获得的利润是元；
2. （2）该经销商购进的第二批杨梅为800千克，获利4800元，求其中售出“特优”和“普通”杨梅各多少千克？
3. （3）该经销商希望自己第三批杨梅的销售的利润率不少于35%，他收购杨梅时要确保能分拣出“特优”杨梅占收购总量的百分比至少要达到多少（精确到1%）？（利润＝销售收入﹣总成本，利润率＝ $\text{[math]}$ ×100%）
答案解析收藏纠错 + 选题