点A,C分别转到了点C,A处,
而点B转到了点D处.
∵ ,
∴四边形 是平行四边形.
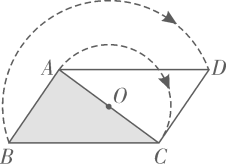
小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是( )
解:由实数的运算法则:“两数相乘,同号得正”
得① ,或②
,
解不等式组①得,x>2,
解不等式组②得,x<﹣3,
所以原不等式的解集为x>2或x<﹣3.
阅读例题,尝试解决下列问题:
例如, 是单项式乘多项式的法则;把这个法则反过来,得到
,这是运用提取公因式法把多项式因式分解.
又如 、
是多项式的乘法公式;把这些公式反过来,得到
、
,这是运用公式法把多项式因式分解.
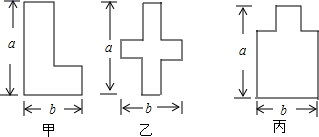
有时在进行因式分解时,以上方法不能直接运用,观察甲、乙两名同学的进行的因式分解.
甲:
(分成两组)
(分别提公因式)
乙:
(分成两组)
(运用公式)
请你在他们解法的启发下,完成下面的因式分解
问题一:因式分解:
对 、
定义一种新运算
,规定:
(其中
,
均为非零常数).当
时,
对任意有理数
、
都成立,试探究
,
的数量关系.
甲说:不可能出现
,所以此题无法解决;
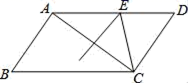
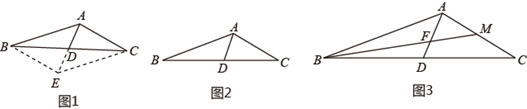
乙说:根据倍长中线法,结合我们新学的平行四边形的性质和判定,我们可延长 至点
,使得
,连接
、
,由于
,所以可得四边形
是平行四边形,请写出此处的依据(平行四边形判定的文字描述)
所以 ,
中,
,
即