山西省晋中市灵石县2019-2020学年九年级上学期数学期末...

更新时间：2021-09-13 浏览次数：58 类型：期末考试

一、单选题

1. (2019九上·灵石期中) 解一元二次方程x²＋4x－1＝0，配方正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 在同一平面直角坐标系中，反比例函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象可能是下面的（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019·武昌模拟) 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为（）

A . 100° B . 110° C . 115° D . 120°

答案解析收藏纠错 + 选题
4. (2019九上·汶上期中) 设A(﹣2，y₁)，B(1，y₂)，C(2，y₃)是抛物线 $\text{[math]}$ 上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A . y₁＞y₂＞y₃ B . y₁＞y₃＞y₂ C . y₃＞y₂＞y₁ D . y₃＞y₁＞y₂

答案解析收藏纠错 + 选题
5. 如图，在△ABC 中，DE∥BC，DF∥AG，若 $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019·大同模拟) 将抛物线y＝x²﹣x+1先向左平移2个单位长度，再向上平移3个单位长度，则所得抛物线的表达式为（）

A . y＝x²+3x+6 B . y＝x²+3x C . y＝x²﹣5x+10 D . y＝x²﹣5x+4

答案解析收藏纠错 + 选题
7. 如图，在山坡上种树，坡度 $\text{[math]}$ ，则相邻两树的水平距离 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019·山西) 北中环桥是省城太原的一座跨汾河大桥(如图1)，它由五个高度不同，跨径也不同的抛物线型钢拱通过吊桥，拉锁与主梁相连，最高的钢拱如图2所示，此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内，与拱脚所在的水平面相交于A，B两点，拱高为78米(即最高点O到AB的距离为78米)，跨径为90米(即AB=90米)，以最高点O为坐标原点，以平行于AB的直线为 $\text{[math]}$ 轴建立平面直角坐标系，则此抛物线钢拱的函数表达式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 的中点为圆心， $\text{[math]}$ 的长为半径作圆交 $\text{[math]}$ 于点D，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2016·达州)
如图，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：
①abc＞0
②4a+2b+c＞0
③4ac﹣b²＜8a
④ $\text{[math]}$ ＜a＜ $\text{[math]}$
⑤b＞c．
其中含所有正确结论的选项是（　　）

A . ①③ B . ①③④ C . ②④⑤ D . ①③④⑤

答案解析收藏纠错 + 选题

二、填空题

11. 计算 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. 如图，在一块长12m，宽8m的矩形空地上，修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行)，剩余部分栽种花草，且栽种花草的面积77m²，设道路的宽为x m，则根据题意，可列方程为.

答案解析收藏纠错 + 选题
13. 如图，在平面直角坐标系中，以坐标原点O为位似中心在y轴的左侧将 $\text{[math]}$ 缩小得到 $\text{[math]}$ ，若 $\text{[math]}$ 与 $\text{[math]}$ 的相似比为2：1，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
14. (2019·山西) 如图，在平面直角坐标系中，点O为坐标原点，菱形ABCD的顶点B在x轴的正半轴上，点A坐标为(-4，0)，点D的坐标为(-1，4)，反比例函数 $\text{[math]}$ 的图象恰好经过点C，则k的值为.

答案解析收藏纠错 + 选题
15. (2021九上·浦北期末) 甲、乙两人进行羽毛球比赛，甲发出一颗十分关键的球，出手点为 $\text{[math]}$ ，羽毛球飞行的水平距离 $\text{[math]}$ （米）与其距地面高度 $\text{[math]}$ （米）之间的关系式为 $\text{[math]}$ ，如图，已知球网 $\text{[math]}$ 距原点 $\text{[math]}$ 米，乙（用线段 $\text{[math]}$ 表示）扣球的最大高度为 $\text{[math]}$ 米，设乙的起跳点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题

三、解答题

16. 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. 学校组织首届“数学文化节”活动，旨在引导同学们感受数学魅力，提升数学素养，活动中，九年级全体同学参加了“趣味数学知识竞赛”．活动中获得“数学之星”称号的小颖得到了 $\text{[math]}$ 四枚纪念章，（除头像外完全相同），如图所示，四枚纪念章上分别印有四位数学家的头像，她将纪念章背面朝上放在桌面上，然后从中随机选取两枚送给妹妹，求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率．（提示：答题时可用序号 $\text{[math]}$ 表示相应的纪念章）

答案解析收藏纠错 + 选题

18. 借鉴我们已有研究函数的经验，探索函数 $\text{[math]}$ 的图像与性质，研究过程如下，请补充完整．

（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

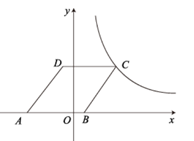
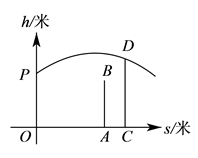
$\text{[math]}$	$\text{[math]}$	-3	-2	-1	0	1	2	3	4	5	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	10	m	-2	1	n	1	-2	3	10	$\text{[math]}$

其中，m=，n=；

（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出函数图象；
（3）观察函数图象：
①写出函数的一条图像性质：；

②当方程 $\text{[math]}$ 有且仅有两个不相等的实数根，根据函数图象直接写出b的取值范围为．

答案解析收藏纠错 + 选题

19. (2019·山西模拟) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象分别交x轴、y轴于A、B两点，与反比例函数 $\text{[math]}$ 的图象交于C、D两点.已知点C的坐标是（6，-1），D（n，3）.
1. （1）求m的值和点D的坐标.
2. （2）求 $\text{[math]}$ 的值.
3. （3）根据图象直接写出：当x为何值时，一次函数的值大于反比例函数的值？
答案解析收藏纠错 + 选题
20. (2019·山西) 某“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制订了测量方案，并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表(不完整)
1. （1）任务一：两次测量A，B之间的距离的平均值是m.
2. （2）任务二：根据以上测量结果，请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
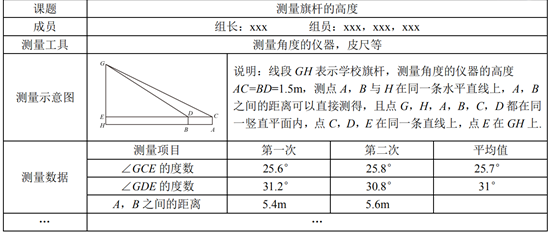
  (参考数据：sin25.7°≈0.43，cos25.7°≈0.90，tan25.7°≈0.48，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60)
3. （3）任务三：该“综合与实践”小组在定制方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳.你认为其原因可能是什么？(写出一条即可).
答案解析收藏纠错 + 选题
21. 已知：如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于D，E是 $\text{[math]}$ 的中点， $\text{[math]}$ 与 $\text{[math]}$ 的延长线相交于点F．
1. （1）求证： $\text{[math]}$ 为 $\text{[math]}$ 的切线；
2. （2）求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2020·硚口模拟) 某超市销售一种文具，进价为 5（元/件），售价为6（元/件）时，当天的销售量为100件，在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件，设当天销售单价统一为 $\text{[math]}$ （元/件）（ $\text{[math]}$ ，且 $\text{[math]}$ 是按0.5元的倍数上涨），当天销售利润为 $\text{[math]}$ 元.
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式（不要求写出自变量的取值范围）；
2. （2）要使当天销售利润不低于240元，求当天销售单价的范围；
3. （3）若每件文具的利润不超过60%，要使当天获得利润最大，每件文具售价为多少元？并求出最大利润.
答案解析收藏纠错 + 选题
23. 如图，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ 、B两点，与y轴交于点C，抛物线的对称轴为直线 $\text{[math]}$ ，交抛物线于点D，交x轴于点E．
　　　　　　　　
1. （1）求抛物线的函数表达式及点B、点D的坐标；
2. （2）抛物线对称轴上的一动点P从点D出发，以每秒1个单位的速度向上运动，连接 $\text{[math]}$ ， $\text{[math]}$ ，设运动时间为 $\text{[math]}$ 秒（ $\text{[math]}$ ），在点P的运动过程中，请求出：当 $\text{[math]}$ 为何值时， $\text{[math]}$ ？
3. （3）若点Q在抛物线上B、C两点之间运动（点Q不与点B、C重合），在运动过程中，设点Q的横坐标为t， $\text{[math]}$ 的面积为S，求S关于t的函数关系式，并求t为何值时S有最大值，最大值是多少？
答案解析收藏纠错 + 选题