 B .
B .  C .
C .  D .
D . 
![]()
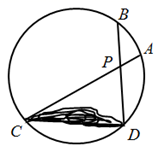
求作:以 为斜边的直角
,使得一个内角等于30°.
作法:①作线段 的垂直平分线交
于点
;
②以点 为圆心,
长为半径画圆;
③以点 为圆心,
长为半径画弧,与
相交,
记其中一个交点为 ;
④分别连接 .
就是所求作的直角三角形.
证明:连接 ,
是
的直径,
▲ °( ▲ )(填推理的依据).
是以
为斜边的直角三角形.
,
是等边三角形.
.
▲ °.
①求 的取值范围;
②写出一个满足条件的 的值,并求此时方程的根.
① 的长为;
②延长 至点
,使得
,此时
与
的数量关系是,
与
的数量关系是;
①按要求补全图形;
②求 的长.
给出如下定义:记线段 的中点为
,当点
不在
上时,平移线段
,使点
落在
上,得到线段
(
分别为点
的对应点)线段
长度的最小值称为线段
到
的“平移距离”.
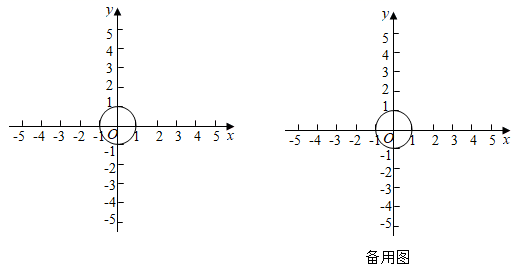
①若点 与原点
重合,则线段
到
的“平移距离”为;
②若线段 到
的“平移距离”为2,则点
的坐标为;