河南省南阳市南召县2021-2022学年九年级上学期期末数学...

更新时间：2022-03-30 浏览次数：74 类型：期末考试

一、单选题

1. (2023九上·六盘水月考) 下列各式化简后的结果为3 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·南召期末) 方程 $\text{[math]}$ 的根是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·南召期末) 如图，在平面直角坐标系中，将 $\text{[math]}$ OAB以原点O为位似中心放大后得到 $\text{[math]}$ OCD，若B（0，1），D（0，3），则 $\text{[math]}$ OAB与 $\text{[math]}$ OCD的面积比是（）

A . 2：1 B . 1：3 C . 1：9 D . 9：1

答案解析收藏纠错 + 选题
4. (2023九上·椒江月考) 将二次函数y=x²﹣2x+3化为y=（x﹣h）²+k的形式，结果为（）

A . y=（x+1）²+4 B . y=（x﹣1）²+4 C . y=（x+1）²+2 D . y=（x﹣1）²+2

答案解析收藏纠错 + 选题
5. (2021九上·衢江期末) 如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC=α ， ∠ADC=β ，则竹竿AB与AD的长度之比为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·汉川月考) 已知(﹣3， $\text{[math]}$ )，(﹣2， $\text{[math]}$ )，(1， $\text{[math]}$ )是抛物线 $\text{[math]}$ 上的点，则（）

A . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ C . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ D . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·绵竹月考) 用※定义一种新运算：对于任意实数m和n，规定m※n＝m²n－mn－3n，如：1※2＝1²×2－1×2－3×2＝－6.则（－2）※ $\text{[math]}$ 结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

8. (2021九上·南召期末) 在大力发展现代化农业的形势下，现有 $\text{[math]}$ 、 $\text{[math]}$ 两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培育环境中分别实验，实验情况记录如下：

种子数量		100	300	500	1000	3000
$\text{[math]}$	出芽率	0.99	0.94	0.96	0.98	0.97
$\text{[math]}$	出芽率	0.99	0.95	0.94	0.97	0.96

下面有三个推断：

①当实验种子数量为100时，两种种子的出芽率均为0.99，所以 $\text{[math]}$ 、 $\text{[math]}$ 两种新玉米种子出芽的概率一样；

②随着实验种子数量的增加， $\text{[math]}$ 种子出芽率在0.97附近摆动，显示出一定的稳定性，可以估计A种子出芽的概率是0.97；

③在同样的地质环境下播种， $\text{[math]}$ 种子的出芽率可能会高于 $\text{[math]}$ 种子．其中合理的是（）

A . ①②③ B . ①② C . ①③ D . ②③

答案解析收藏纠错 + 选题

9. (2022九上·沈阳期末) 二次函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象是抛物线G，自变量x与函数y的部分对应值如下表：

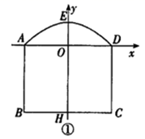
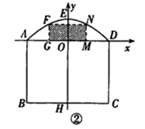
x	…	﹣5	﹣4	﹣3	﹣2	﹣1	0	…
y	…	4	0	﹣2	﹣2	0	4	…

下列说法正确的是（）

A . 抛物线G的开口向下 B . 抛物线G的对称轴是直线 $\text{[math]}$ C . 抛物线G与y轴的交点坐标为（0，4） D . 当x＞﹣3时，y随x的增大而增大

答案解析收藏纠错 + 选题

10. (2021九上·南召期末) 如图，已知菱形OABC的顶点O（0，0），B（2，2），菱形的对角线的交于点D；若将菱形OABC绕点O逆时针旋转，每秒旋转45°，从如图所示位置起，经过60秒时，菱形的对角线的交点D的坐标为（）

A . （1，1） B . （﹣1，﹣1） C . （-1，1） D . （1，﹣1）

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·南召期末) 林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：
移植的棵数n
1000
1500
2500
4000
8000
15000
20000
30000
成活的棵数m
865
1356
2220
3500
7056
13170
17580
26430
成活的频率 $\text{[math]}$
0.865
0.904
0.888
0.875
0.882
0.878
0.879
0.881
估计该种幼树在此条件下移植成活的概率为．

答案解析收藏纠错 + 选题
12. (2022九上·历城期中) 如图，为了测量操场上一棵大树的高度，小英拿来一面镜子，平放在离树根部5m的地面上，然后她沿着树根和镜子所在的直线后退，当她后退1m时，正好在镜中看见树的顶端．小英估计自己的眼睛到地面的距离为1.6m，则大树的高度是m．

答案解析收藏纠错 + 选题
13. (2021九上·南召期末) 在平面直角坐标系 $\text{[math]}$ 中，过点P（0，2）作直线 $\text{[math]}$ （b为常数且b<2）的垂线，垂足为点 $\text{[math]}$ ，则sin∠OPQ=.

答案解析收藏纠错 + 选题
14. (2021九上·南召期末) 如图，已知函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，点 $\text{[math]}$ 的纵坐标为1，则关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的解为.

答案解析收藏纠错 + 选题
15. (2024九下·渠县期中) 点P（m，n）在以y轴为对称轴的二次函数y=x²+ax+4的图象上，则m-n的最大值为.

答案解析收藏纠错 + 选题

三、解答题

16. (2021九上·南召期末)
1. （1）计算：4sin30°﹣ $\text{[math]}$ cos45°﹣ $\text{[math]}$ tan30°+2sin60°
2. （2）计算： $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2021九上·南召期末) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ ．
1. （1）若方程有两个相等的实数根用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ；
2. （2）若方程有两个不相等的实数根，且 $\text{[math]}$ ．
  ①求 $\text{[math]}$ 的取值范围；
  
  ②写出一个满足条件的 $\text{[math]}$ 的值，并求此时方程的根．
答案解析收藏纠错 + 选题

18. (2021九上·南召期末) 根据公安部交管局下发的通知，春节前开展一次“一带一盔”安全守护行动，其中要求骑行摩托车、电动车需要佩戴头盔，某日交警部门在某个十字路口共拦截了50名不带头盔的骑行者，根据年龄段和性别得到如下表的统计信息，根据表中信息回答下列问题：

年龄x（岁）	人数	男性占比
x＜20	4	50%
20≤x＜30	m	60%
30≤x＜40	25	60%
40≤x＜50	8	75%
x≥50	3	100%

（1）统计表中m的值为；
（2）若要按照表格中各年龄段的人数来绘制扇形统计图，则年龄在“30≤x＜40”部分所对应扇形的圆心角的度数为；
（3）若从年龄在“x＜20”的4人中随机抽取2人参加交通安全知识学习，请用列表或画树状图的方法，求恰好抽到1名男性和1名女性的概率.

答案解析收藏纠错 + 选题

19. (2021九上·南召期末) 如图，在 $\text{[math]}$ ABC中，点D，E分别在边AB，AC上，连接DE.
1. （1）若AD•AB＝AE•AC.求证： $\text{[math]}$ ADE∽ $\text{[math]}$ ACB；
2. （2）若AB=8，AC=6，AD=3，直接写出：当AE=时， $\text{[math]}$ ADE与 $\text{[math]}$ ACB相似.
答案解析收藏纠错 + 选题
20. (2021九上·南召期末) （材料阅读）2020年5月27日，2020珠峰高程测量登山队成功登顶珠穆朗玛峰，将用中国科技“定义”世界新高度，其基本原理之一是三角高程测量法，在山顶上立一个标杆，找到2个以上测量点，分段测量山的高度，再进行累加.因为地球面并不是水平的，光线在空气中会发生折射，所以当两个测量点的水平距离大于300m时，还要考虑球气差，球气差计算公式为 $\text{[math]}$ （其中d为两点间的水平距离，R为地球的半径，R取6400000m），即：山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.
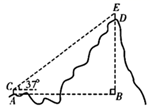
（问题解决）某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图，点A，B的水平距离d=800m，测量仪AC=1.5m，觇标DE=2m，点E，D，B在垂直于地面的一条直线上，在测量点A处用测量仪测得山顶标杆顶端E的仰角为37°，测量点A处的海拔高度为1800m.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）.请你计算该山的海拔高度（要计算球气差，结果精确到0.01m）.

答案解析收藏纠错 + 选题
21. (2021九上·南召期末) 某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙，它由长方形和抛物线构成，长方形的长AD=4米，宽AB=3米，抛物线的最高点E到BC的距离为4米.
1. （1）按如图①所示的直角坐标系，抛物线可以用 $\text{[math]}$ 表示.直接写出抛物线的函数表达式 .
2. （2）现将A型活动板房改造为B型活动板房.如图②，在抛物线与AD之间的区域内加装一扇长方形窗户FGMN，点G，M在AD上，点N，F在抛物线上，窗户每平方米的成本为50元.已知GM=2米，直接写出：每个B型活动板房的成本是元.（每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本）
3. （3）根据市场信息，这样的B型活动板房公司每月最多能生产 $\text{[math]}$ 个，若以单价 $\text{[math]}$ 元销售B型活动板房，每月能售出 $\text{[math]}$ 个；若单价每降低 $\text{[math]}$ 元，每月能多售出 $\text{[math]}$ 个这样的B型活动板房.不考虑其他因素，公司将销售单价 $\text{[math]}$ （元）定为多少时，每月销售B型活动板房所获利润 $\text{[math]}$ （元）最大？最大利润是多少？
答案解析收藏纠错 + 选题
22. (2021九上·南召期末) 如图，已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ABC的三个顶点，其中点A（0，1），点B（-9，10）， $\text{[math]}$ 轴，点P是直线AC下方抛物线上的动点.
1. （1）直接写出：b= ，c=；
2. （2）过点P且与y轴平行的直线l与直线AB，AC分别交于点E，F，当四边形AECP的面积最大时，求点P的坐标；
3. （3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C，P，Q为顶点的三角形与 $\text{[math]}$ ABC相似，若存在，直接写出点Q的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题
23. (2021九上·南召期末) 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ 为斜边 $\text{[math]}$ 上一动点，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，使得点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）如图①，若 $\text{[math]}$ ，证明： $\text{[math]}$ .
2. （2）如图②，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
3. （3）如图③，若 $\text{[math]}$ ，是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ .若存在，求此时 $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省南阳市南召县2021-2022学年九年级上学期期末数学...

副标题：

*注意事项：

河南省南阳市南召县2021-2022学年九年级上学期期末数学...

试题分析

总体分析

题量分析

难度分析

知识点分析

移植的棵数n	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数m	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\text{[math]}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881