



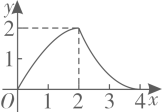
 B .
B . 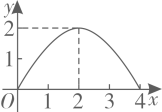 C .
C .  D .
D . 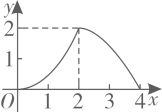

|
摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
摸到黑球的次数m |
73 |
113 |
154 |
370 |
604 |
751 |
|
摸到黑球的频率 | 0.73 | 0.753 | 0.77 | 0.74 | 0.755 | 0.751 |

