| 甲 | 乙 | 丙 | 丁 | |
| 平均分 | 85 | 90 | 90 | 85 |
| 方差 | 50 | 42 | 50 | 42 |
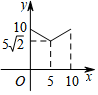 B .
B . 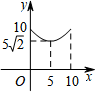 C .
C . 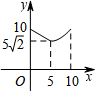 D .
D . 


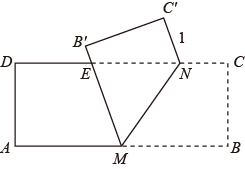
| 课题 | 测量河流宽度 | ||
| 测量工具 | 测量角度的仪器,皮尺等 | ||
| 测量小组 | 第一小组 | 第二小组 | 第三小组 |
| 测量方案示意图 | | | |
| 说明 | 点 | 点 | 点 |
| 测量数据 | | | |
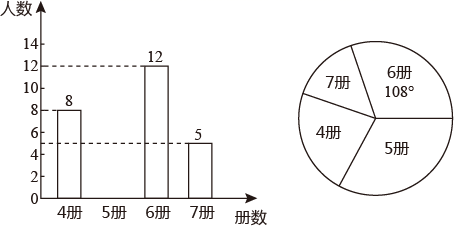
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
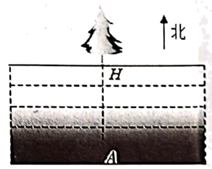
|
|
14 |
15 |
16 |
17 |
18 |
14.4 |
12 |
10.3 |
9 |
8 |
7.2 |

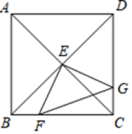
截长补短法,是初中数学几何题中一种输助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.

解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是