河南省南阳市中原名校2020-2021学年数学中考第二次大联...

更新时间：2021-11-19 浏览次数：146 类型：中考模拟

一、单选题

1. (2022·金东模拟) ﹣2的绝对值是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . -2

答案解析收藏纠错 + 选题
2. (2021·南阳模拟) 2021年3月5日，李克强总理在政府工作报告中指出，过去五年，我国国民生产总值从不到70万亿元增加到了100万亿元.100万亿用科学记数法表示正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·南阳模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·南阳模拟) 在体育模拟测试中，某班10名学生的成绩分别是60，58，62，66，68，66，67，63，69，65，这组数据的众数和中位数分别是（）

A . 66，65 B . 66， $\text{[math]}$ C . 66，66 D . 66，67

答案解析收藏纠错 + 选题
5. (2021·南阳模拟) 如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 36° B . 41° C . 46° D . 51°

答案解析收藏纠错 + 选题
6. (2021·南阳模拟) 下列关于二次函数 $\text{[math]}$ 的说法正确的是（）

A . 该函数图象的开口向上 B . 该函数图象的顶点坐标为 $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小 D . 该函数的最大值为7

答案解析收藏纠错 + 选题
7. (2023九上·榆树月考) 某校初三年级举行班级篮球友谊赛，每两个班都要进行一场比赛，张老师告诉小丽总共要进行120场比赛，小丽想通过列方程求出参与比赛的班级数.设参与比赛的班级有 $\text{[math]}$ 个，则所列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·南阳模拟) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别是对角线 $\text{[math]}$ ， $\text{[math]}$ 的中点，则 $\text{[math]}$ 的长为（）

A . 1 B . 1.5 C . 2.5 D . 3.5

答案解析收藏纠错 + 选题
9. (2021·南阳模拟) 如图，点 $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上， $\text{[math]}$ 的延长线交 $\text{[math]}$ 轴于点 $\text{[math]}$ .已知 $\text{[math]}$ ， $\text{[math]}$ 的面积为6，则 $\text{[math]}$ 的值为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
10. (2021·南阳模拟) 如图，等边三角形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，点 $\text{[math]}$ 是边 $\text{[math]}$ 上的一动点，作射线 $\text{[math]}$ .射线 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转60°得到射线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则点 $\text{[math]}$ 从 $\text{[math]}$ 的运动过程中， $\text{[math]}$ 的最大值是（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022八下·金华月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2021·南阳模拟) 不等式 $\text{[math]}$ 的最小整数解是.

答案解析收藏纠错 + 选题
13. (2021·南阳模拟) 如图， $\text{[math]}$ 的三个内角满足 $\text{[math]}$ .分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于点 $\text{[math]}$ ， $\text{[math]}$ ，作直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2021·南阳模拟) 五张完全相同的卡片上分别写有数字1， $\text{[math]}$ ， $\text{[math]}$ ，2， $\text{[math]}$ .闭上眼睛洗匀后随机抽取三张，以卡片上的数字作为三角形的三边，所得三角形恰好是直角三角形的概率为.

答案解析收藏纠错 + 选题
15. (2021·南阳模拟) 如图，在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为斜边作等腰直角三角形 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题

三、解答题

16. (2021·南阳模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2021·南阳模拟) 近几年，研学旅行已成为中小学广泛开展的课外拓展活动.某学校认真策划研学旅行活动，有针对性地开发了自然、历史、地理、科技、人文、体验等六种类型的活动课程.为了了解同学们选择课程的情况，校园小记者随机调查了本校部分同学，根据调查结果绘制出了如下两个尚不完整的统计图.

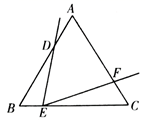
请结合图中所给信息，解答下列问题：
1. （1）这次被调查的学生共有人；
2. （2）求扇形统计图中“历史”所对应的圆心角的度数，并补全条形统计图；
3. （3）若全校共有5000人，请你估计选择“体验”类课程的学生人数.
答案解析收藏纠错 + 选题
18. (2021·南阳模拟) 位于河南省登封市境内的嵩岳寺塔是中国现存最早的砖塔，反映了中外建筑文化交流融合创新的历程，在结构、造型等方面具有很大价值，对后世砖塔建筑有着巨大影响.

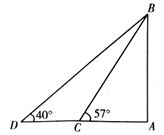
清明假期，小红利用所学知识来测量塔的高度，测角仪和塔底 $\text{[math]}$ 在同一水平面，如图，她先在 $\text{[math]}$ 处测得塔顶 $\text{[math]}$ 的仰角为57°，然后沿直线 $\text{[math]}$ 向远离塔的方向前进20米到达 $\text{[math]}$ 处，测得塔顶 $\text{[math]}$ 的仰角为40°.求嵩岳寺塔的高度.（结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
19. (2021·南阳模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点.以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求阴影部分的面积.
答案解析收藏纠错 + 选题
20. (2021·南阳模拟) 为了保障羊肉正常供应，某畜牧集团的 $\text{[math]}$ ， $\text{[math]}$ 两个养殖场共出栏肥羊2000只， $\text{[math]}$ 养殖场的肥羊数量是 $\text{[math]}$ 养殖场的2倍少400只.这批肥羊将运往甲地1300只，乙地700只，运费如下表（单位：元/只）

养殖场

目的地

$\text{[math]}$

$\text{[math]}$

甲

25

18

乙

20

24
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 养殖场各出栏多少只肥羊？
2. （2）设这批肥羊从 $\text{[math]}$ 养殖场运往甲地 $\text{[math]}$ 只 $\text{[math]}$ ，全部运往甲、乙两地的总费用为 $\text{[math]}$ 元，求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式，并设计使总运费最少的调运方案；
3. （3）当每只肥羊的运费下降 $\text{[math]}$ 元（ $\text{[math]}$ 且 $\text{[math]}$ 为整数）时，按（2）中设计的调运方案，总运费不超过30000元，求 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
21. (2021·南阳模拟) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，已知 $\text{[math]}$ ，且 $\text{[math]}$ 的面积为 $\text{[math]}$ .
1. （1）求抛物线的解析式；
2. （2）点 $\text{[math]}$ 是直线 $\text{[math]}$ 上方抛物线上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，交直线 $\text{[math]}$ 于点 $\text{[math]}$ .抛物线上是否存在点 $\text{[math]}$ ，使以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是平行四边形？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
22. (2021·南阳模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 为直线 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ .过点 $\text{[math]}$ 作 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）如图1，若 $\text{[math]}$ ，当点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ ；
2. （2）如图2，若 $\text{[math]}$ ，当点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上时，设 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长（用含 $\text{[math]}$ ， $\text{[math]}$ 的式子表示）；
3. （3）如图3，若 $\text{[math]}$ ，当点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上时，用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并证明.
答案解析收藏纠错 + 选题

23. (2021·南阳模拟) 小亮在学习中遇到如下一个问题：

如图1，点 $\text{[math]}$ 是半圆 $\text{[math]}$ 上一动点，线段 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .当 $\text{[math]}$ 为等腰三角形时，求线段 $\text{[math]}$ 的长度.

小亮分析发现，此问题很难通过常规的推理计算彻底解决，于是他尝试结合学习函数的经验研究此问题.将线段 $\text{[math]}$ 的长度作为自变量 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 的长度都是 $\text{[math]}$ 的函数，分别记为 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ .请将下面的探究过程补充完整：

（1）根据点 $\text{[math]}$ 在半圆 $\text{[math]}$ 上的不同位置，画出相应的图形，测量线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的长度，得到下表的几组对应值：

$\text{[math]}$	0	1.0	2.0	3.0	4.0	4.5	5.0	5.5	6
$\text{[math]}$	6	5.9	5.7	5.2	4.5	$\text{[math]}$	3.3	2.4	0
$\text{[math]}$	6	5.0	4.2	3.7	4	4.5	5.3	6.3	8.5

①上表中 $\text{[math]}$ 的值是 ▲ ；

②操作中发现，“无需测量线段 $\text{[math]}$ 的长度即可得到 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式”.请直接写出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式.

（2）小亮已在平面直角坐标系 $\text{[math]}$ 中画出了函数 $\text{[math]}$ 的图象，如图2所示.

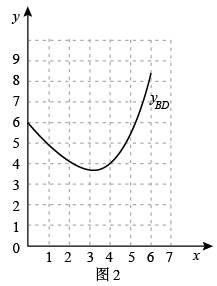
①请在同一坐标系中画出函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象；

②结合图象直接写出当 $\text{[math]}$ 为等腰三角形时，线段 $\text{[math]}$ 长度的近似值（结果保留一位小数）
（3）小亮观察发现，函数 $\text{[math]}$ 的图象有最低点.请你直接写出线段 $\text{[math]}$ 长度的最小值（写出精确值）

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省南阳市中原名校2020-2021学年数学中考第二次大联...

副标题：

*注意事项：

河南省南阳市中原名校2020-2021学年数学中考第二次大联...

试题分析

总体分析

题量分析

难度分析

知识点分析