![]()
![]()
![]()
| 甲 | 乙 | 丙 | 丁 | |
| 平均分`x | 90 | 87 | 90 | 87 |
| 方差S2 | 12.5 | 13.5 | 1.4 | 1.4 |
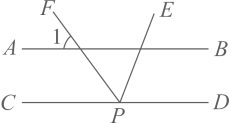
 B .
B . 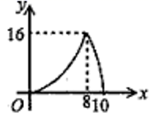 C .
C . 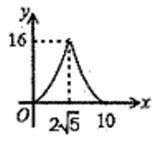 D .
D . 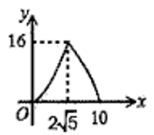

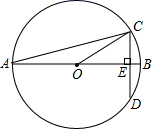


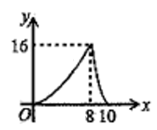
①当n =2时,求线段CD的长;
②若CD OB,结合函数的图象,直接写出 n的取值范围.
七年级10名学生的竞赛成绩是:98,80,98,86,98,96,90,100,89,82
八年级10名学生的竞赛成绩在C组中的数据是:94,90,94
八年级抽取的学生竞赛成绩扇形统计图

七,八年级抽取的学生竞赛成绩统计表
| 年级 | 七年级 | 八年级 |
| 平均数 | 92 | 92 |
| 中位数 | 93 | |
| 众数 | | 100 |
根据以上信息,解答下列问题:


①在(-3,-1),(2,2),(3,3)中,是点A的“正轨点”的坐标是 .
②若点A的“正轨正方形”的面积是4,写出一个点A的“正轨点”的坐标.