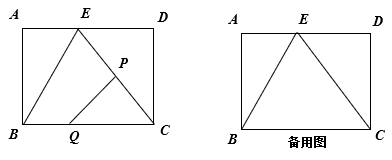
B .
B .  C .
C .  D .
D . 




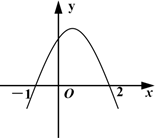

⑴阅读下面的材料:
如果函数 =f(
)满足:对于自变量x的取值范围内的任意
,
,
①若 <
,都有f(
)<f(
),则称f(
)是增函数;
②若 <
,都有f(
)>f(
),则称f(
)是减函数.
例题:证明函数f( )=
(
>0)是减函数.
证明:设0< <
,
f( )﹣f(
)=
=
=
.
∵0< <
,
∴ ﹣
>0,
>0.
∴ >0.即f(
)﹣f(
)>0.
∴f( )>f(
).
∴函数f( )=
(
>0)是减函数.
⑵根据以上材料,解答下面的问题:
已知:函数f( )=
(
<0),
①计算:f(﹣1)= ▲ , f(﹣2)= ▲ ;
②猜想:函数f( )=
(
<0)是 ▲ 函数(填“增”或“减”);
③验证:请仿照例题证明你对②的猜想.