
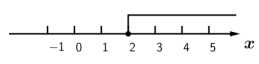
 B .
B .  C .
C . 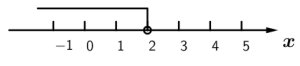
 B .
B .  C .
C .  D .
D . 

Ⅰ、数据收集,从全校随机抽取20学生,进行每周用于课外阅读时间的调查,数据如下(单位:):
|
30 |
60 |
81 |
50 |
44 |
110 |
130 |
146 |
80 |
100 |
|
60 |
80 |
120 |
140 |
75 |
81 |
10 |
30 |
81 |
92 |
Ⅱ、整理数据,按如下分段整理样本数据并补全表格:
|
课外阅读时间 |
|
|
|
|
|
等级 |
|
|
|
|
|
人数 |
3 |
|
8 |
|
Ⅲ、分析数据,补全下列表格中的统计量:
|
平均数 |
中位数 |
众数 |
|
80 |
|
81 |
Ⅳ、得出结论:

教材分析:如图,是⊙O的直径,
是直径
所对的圆周角,根据上述定理,则
, 如果我们把
看作是180°的圆心角,可以进一步得到的结论:
, 即:半圆所对的圆周角等于该半圆所对的圆心角的一半.

联想猜测:那么对于非半圆所对的圆周角,是不是也有类似的规律呢?
探究化归:不难发现,按圆心与圆周角的位置关系分类,我们可将圆周角分为三类.

②圆心在圆周角内,如图②,我们将其化归为①的情形,作直径 . 由①的结论,
,
.
(∠+∠)
.
