

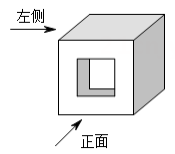
 B .
B .  C .
C .  D .
D . 




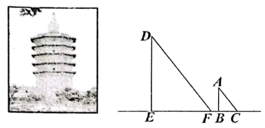
| 三国时期的数学家赵爽在其所落的《勾股圆方图注》中记载了一元二次方程的几何解法,以
将方程
可得新方程:
∵x表示边长, ∴
∴
|
任务一:①这种构造图形解一元二次方程的方法体现的数学思想是 ;
A.分类讨论思想 B.数形结合思想 C.演绎思想 D.公理化思想
②用配方法解方程:
.
任务二:比较上述两种解一元二次方程的方法,请反思利用构造图形的方法求解一元二次方程的不足之处是 . (写出一条即可)

如图1,腾飞小组将矩形纸片折叠,点A落在
边上的点
处,折痕为
, 连接
, 然后将纸片展平,得到四边形
. 试判断四边形
的形状,并加以证明.
①求的面积;
②连接 , 线段
与线段
交于点M,则
▲ .
如图3,探究小组将图1的四边形剪下,在边
上取一点N,使
, 将
沿线段
折叠得到
, 连接
, 探究并直接写出
的长度.
①填空:点D的坐标为 ▲ , 点E的坐标为 ▲ ;
②请判断线段与
的位置关系,并说明理由.
①求k的值;
②若动点M在y轴上运动,当线段与
的差最大时,请直接写出点M的坐标.