河南省南阳市第十三中学校2021-2022学年八年级上学期第...

更新时间：2022-03-24 浏览次数：74 类型：月考试卷

一、单选题

1. 下列命题中是真命题的是（）

A . 对顶角相等 B . 两点之间，直线最短 C . 同位角相等 D . 同旁内角互补

答案解析收藏纠错 + 选题
2. 满足下列条件的 $\text{[math]}$ ，不是直角三角形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 如图，某同学把一块三角形的玻璃块打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（）

A . 带①去 B . 带②去 C . 带③去 D . 带①②去

答案解析收藏纠错 + 选题
4. 三角形的三边长分别为a，b，c，且满足 $\text{[math]}$ ，则该三角形的形状是（）

A . 任意等腰三角形 B . 等腰直角三角形 C . 等腰三角形或直角三角形 D . 任意直角三角形

答案解析收藏纠错 + 选题
5. 用反证法证明“ 在同一平面内，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ”时，应假设（）

A . a不垂直于c B . a，b都不垂直于c C . $\text{[math]}$ D . a与b相交

答案解析收藏纠错 + 选题
6. (2020八上·盐湖期末) 如图所示， $\text{[math]}$ 是长方形地面，长 $\text{[math]}$ ，宽 $\text{[math]}$ ，中间整有一堵砖墙高 $\text{[math]}$ ，一只蚂蚁从A点爬到C点，它必须翻过中间那堵墙，则它至少要走（）

A . 20 B . 24 C . 25 D . 26

答案解析收藏纠错 + 选题
7. 如图所示，甲渔船以8海里/时的速度离开港口O向东北方向航行，乙渔船以6海里/时的速度离开港口O向西北方向航行，他们同时出发，一个半小时后，甲、乙两渔船相距（）

A . 12海里 B . 13海里 C . 14海里 D . 15海里

答案解析收藏纠错 + 选题
8. 如图，在 $\text{[math]}$ 中，分别以点A和B为圆心，大于 $\text{[math]}$ 和长为半径画弧，两弧相交于点M，N，作直线 $\text{[math]}$ ，交 $\text{[math]}$ 于点D，连接 $\text{[math]}$ ，若 $\text{[math]}$ 的周长为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的周长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019·衢州) “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）

A . 60° B . 65° C . 75° D . 80°

答案解析收藏纠错 + 选题
10. 如图，在 $\text{[math]}$ 中 $\text{[math]}$ ， $\text{[math]}$ ，D，E是BC上两点，且 $\text{[math]}$ ，过点A作 $\text{[math]}$ ，垂足是A，过点C作 $\text{[math]}$ ，垂足是C，CF交AF于点F，连接EF.给出下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；④ $\text{[math]}$ .其中正确结论的字号是（）

A . ①②③ B . ②③④ C . ①③④ D . ①②④

答案解析收藏纠错 + 选题

二、填空题

11. 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是.

答案解析收藏纠错 + 选题
13. (2018八上·长春期末) 如图所示的一块地，已知∠ADC＝90°，AD＝12m，CD＝9m，AB＝25m， BC＝20m，则这块地的面积为

答案解析收藏纠错 + 选题
14. 如图，在长方形ABCD中， $\text{[math]}$ ， $\text{[math]}$ .延长BC到点E，使 $\text{[math]}$ ，连结DE，动点P从点B出发，以每秒2个单位长度的速度沿 $\text{[math]}$ 向终点A运动.设点P的运动时间为t秒，当t的值为时， $\text{[math]}$ 和 $\text{[math]}$ 全等.

答案解析收藏纠错 + 选题
15. 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ，直线EF是AB的垂直平分线，D是BC的中点，M是EF上一个动点， $\text{[math]}$ 的面积为12， $\text{[math]}$ ，则 $\text{[math]}$ 周长的最小值是.

答案解析收藏纠错 + 选题

三、解答题

16. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边分别是a，b，c，根据下列各边的长度，判断各三角形是否为直角三角形.并指出哪一个角是直角.
1. （1） $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2） $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2016七下·普宁期末) 已知∠MAN．
1. （1）用尺规完成下列作图：（保留作图痕迹，不写作法）
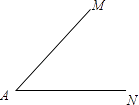
  ①作∠MAN的平分线AE；
  ②在AE上任取一点F，作AF的垂直平分线分别与AM、AN交于P、Q；
2. （2）在（1）的条件下，线段AP与AQ有什么数量关系，请直接写出结论．
答案解析收藏纠错 + 选题
18. (2020八上·龙岗月考) 八年级1班松松同学学习了“勾股定理”之后，为了测量如图的风筝的高度CE，测得如下数据：

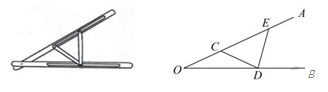
①测得BD的长度为8米：(注：BD⊥CE)

②根据手中剩余线的长度计算出风筝线BC的长为17米；

③牵线放风筝的松松身高1.6米．
1. （1）求风筝的高度CE．
2. （2）若松松同学想风筝沿CD方向下降9米，则他应该往回收线多少米?
答案解析收藏纠错 + 选题
19. (2018·广元) 如图，在△AEC和△DFB中，∠E＝∠F，点A，B，C，D在同一直线上，有如下三个关系式：①AE∥DF，②AB＝CD，③CE＝BF.
1. （1）请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题(用序号写出命题书写形式：“如果⊗，⊗，那么⊗”)；
2. （2）选择(1)中你写出的一个命题，说明它正确的理由．
答案解析收藏纠错 + 选题
20. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿AD折叠，使点C落在AB上的点E处，求DB的长.

答案解析收藏纠错 + 选题
21. 如图，已知AD∥BC，点E是CD上一点，AE平分∠BAD，BF平分∠ABC，延长BE交AD的延长线于点F
1. （1）求证：△ABE≌△AFE；
2. （2）若AD＝2，BC＝6，求AB的长.
答案解析收藏纠错 + 选题
22. 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图①），后人称之为“赵爽弦图”，流传至今.如图①是用四个能够完全重合的直角三角形拼成的图形，其中直角边长分别为a，b，斜边长为c，用含a，b，c的代数式表示：
1. （1）大正方形的面积为；小正方形的面积为；
2. （2）四个直角三角形的面积和为，根据图中面积关系，可列出a，b，c之间的关系式为；
3. （3）如图②，以直角三角形的三边为直径，分别向外部作半圆，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足的关系是；
4. （4）如图③直角三角形的两条直角边长分别为3、5，分别以直角三角形的三边为直径作半圆，则图中两个月形图案（阴影部分）的面积和为.
答案解析收藏纠错 + 选题
23. 已知，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D为BC的中点.
1. （1）观察猜想
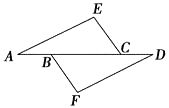
  如图①，若点E、F分别是AB、AC的中点，则线段DE与DF的数量关系是；线段DE与DF的位置关系是.
2. （2）类比探究
  如图②，若点E、F分别是AB、AC上的点，且 $\text{[math]}$ ，上述结论是否仍然成立，若成立，请证明：若不成立，请说明理由；
3. （3）解决问题
  如图③，若点E、F分别为AB、CA延长线的点，且 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题