 B .
B .  C .
C .  D .
D . 
 B .
B . 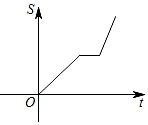 C .
C . 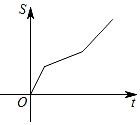 D .
D . 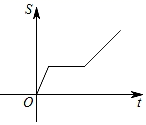
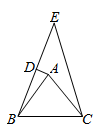




![]()
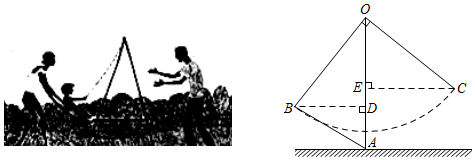
七下教材第149页提出这样一个问题:如图1,∠AOB=90°,OC平分∠AOB,把三角尺的直角顶点落在OC的任意一点P上,并使三角尺的两条直角边分别与OA、OB相交于点E、F,PE与PF相等吗?

①PE与PF还相等吗?为什么?
②试判断OE、OF、OP三条线段之间的数量关系,并说明理由.
①则图中(不添加其他辅助线)与∠EPA相等的角有 ;(都写出来)
②试求线段OQ长的最小值.