 B .
B .  C .
C .  D .
D . 
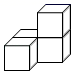
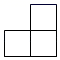 B .
B . 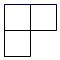 D .
D . 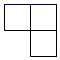





以下是近五年全国及新疆地区棉花播种面积和棉花产量百分比的统计图,请结合统计图回答下列问题:



注:“●”表示服用甲种药物的患者,“▲”表示服用乙种药物的患者.
根据以上信息,回答下列问题:
①药物浓度m低于2的有人;
②将20名服用甲种药物患者的病毒载量m的方差记作S12 , 20名服用乙种药物患者的病毒载量n的方差记作S22 , 则S12S22(填“>”,“=”或“<”);
①药物正式投入市场后,300名服用甲种药物且有效的患者大约有 ▲ 人;
②在服用两种药物“特别有效”的患者中,各随机选取一人进行进一步的检测,已知服用每种药物“特别有效”的患者中的男女比例均为2:1,求正好选到性别不相同的患者的概率是多少?
