湖南省2021-2022学年九年级下学期期中数学试卷

更新时间：2022-04-25 浏览次数：56 类型：期中考试

一、单选题

1. (2022九下·湖南期中) 在四个实数 $\text{[math]}$ ， 0，﹣1， $\text{[math]}$ 中，最大的是（）

A . $\text{[math]}$ B . 0 C . ﹣1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·成都期末) 下列四个几何体中，主视图是三角形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022九下·湖南期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九下·湖南期中) 下列不是必然事件的是（）

A . 角平分线上的点到角两边距离相等 B . 三角形两边之和大于第三边 C . 面积相等的两三角形全等 D . 三角形外心到三个顶点距离相等

答案解析收藏纠错 + 选题
5. (2024八下·青秀期中) 若一次函数 $\text{[math]}$ 的函数值 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九下·湖南期中) 方程 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九下·湖南期中) 如图，在△ABC中，AB＝6，将△ABC绕点A逆时针旋转40°后得到△ADE，点B经过的路径为 $\text{[math]}$ ，则图中阴影部分的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4π D . 条件不足，无法计算

答案解析收藏纠错 + 选题
8. (2024九上·三河期末) 对于题目：在平面直角坐标系中，直线 $\text{[math]}$ 分别与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点，过点 $\text{[math]}$ 且平行 $\text{[math]}$ 轴的直线与过点 $\text{[math]}$ 且平行 $\text{[math]}$ 轴的直线相交于点 $\text{[math]}$ ，若抛物线 $\text{[math]}$ 与线段 $\text{[math]}$ 有唯一公共点，求 $\text{[math]}$ 的取值范围.甲的计算结果是 $\text{[math]}$ ；乙的计算结果是 $\text{[math]}$ ，则（）

A . 甲的结果正确 B . 乙的结果正确 C . 甲与乙的结果合在一起正确 D . 甲与乙的结果合在一起也不正确

答案解析收藏纠错 + 选题

二、填空题

9. (2024七下·海曙期末) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2022九下·湖南期中) 将数字51200000用科学记数法表示为．

答案解析收藏纠错 + 选题
11. (2022九下·湖南期中) 若代数式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
12. (2022九下·湖南期中) 一个正方体盒子的展开图如图所示，如果要把它粘成一个正方体，那么与点A重合的点是点.

答案解析收藏纠错 + 选题
13. (2022九下·湖南期中) 一口袋中装有10个红球和若干个黄球（这些球除颜色外都相同），通过大量重复实验得知，摸到红球的频率为0.4.据此估计：口袋中约有个黄球.

答案解析收藏纠错 + 选题
14. (2022九下·湖南期中) 一个一元二次方程的二次项系数为1，其中一个根是﹣3，另一个根是2，则这个方程是.

答案解析收藏纠错 + 选题
15. (2022九下·湖南期中) 如图，Rt△AOB中，∠OAB＝90°，∠OBA＝30°，顶点A在反比例函数y＝ $\text{[math]}$ 图象上，若Rt△AOB的面积恰好被y轴平分，则进过点B的反比例函数的解析式为.

答案解析收藏纠错 + 选题
16. (2022九下·湖南期中) 在同一条数轴上，点B表示的数是-8，点C表示的数是16，若点B以每秒6个单位长度的速度向右匀速运动，同时点C以每秒2个单位长度的速度向左匀速运动，当运动秒时， $\text{[math]}$ 个单位长度.

答案解析收藏纠错 + 选题

三、解答题

17. (2022九下·湖南期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2022九下·湖南期中) 解不等式组 $\text{[math]}$ 并写出不等式组的整数解.

答案解析收藏纠错 + 选题
19. (2022九下·湖南期中) 化简：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
3. （3）先化简，再从0，1，2中选择一个合适的数代入求值： $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2022九下·湖南期中) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ ，与y轴交于点C，与反比例 $\text{[math]}$ 的图象交于点A.点B为AC的中点.求一次函数 $\text{[math]}$ 和反比例 $\text{[math]}$ 的解析式.

答案解析收藏纠错 + 选题
21. (2022九下·湖南期中) 某公司后勤部准备去超市采购牛奶和咖啡若干箱，现有两种不同的购买方案，如表：

牛奶（箱）
咖啡（箱）
金额（元）
方案一
20
10
1100
方案二
10
20
1300
1. （1）求牛奶与咖啡每箱分别为多少元；
2. （2）超市中该款咖啡和牛奶有部分因保质期临近，进行打六折的促销活动，后勤部根据需要选择原价或打折的咖啡和牛奶，此次采购共花费了1800元，其中购买打折的牛奶箱数是所有牛奶、咖啡的总箱数的 $\text{[math]}$ ，则此次按原价采购的咖啡有箱.（直接写出答案）
答案解析收藏纠错 + 选题
22. (2022九下·湖南期中) 疫情期间，某药店出售一批进价为2元的口罩，在市场营销中发现此口罩的日销售单价x（元）与日销售量y（只）之间有如下关系：

日销售单价x（元）

3

4

5

6

日销售量y（只）

2000

1500

1200

1000
1. （1）猜测并确定y与x之间的函数关系式；
2. （2）设经营此口罩的销售利润为W元，求出W与x之间的函数关系式？
3. （3）若物价局规定此口罩的售价最高不能超过10元/只，请你求出当日销售单价x定为多少时，才能获得最大日销售利润？最大利润是多少元？
答案解析收藏纠错 + 选题

23. (2022九下·湖南期中) 某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法，做了一次抽样调查，调查结果共分为四个等级：A．非常了解：B．比较了解：C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的三种统计图表．请结合统计图表，回答下列问题：

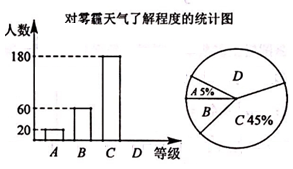
	对雾霾的了解程度	百分比
A	非常了解	5%
B	比较了解	m%
C	基本了解	45%
D	不了解	n%

（1）本次参与调查的市民共有人，m=，n=．
（2）统计图中扇形D的圆心角是度。
（3）某校准备开展关于雾霾的知识竞赛，九（3）班郑老师欲从2名男生和1名女生中任选2人参加比赛，求恰好选中“1男1女”的概率（要求列表或画树状图）．

答案解析收藏纠错 + 选题

24. (2022九下·湖南期中) 海鲜门市的某种海鲜食材，成本为10元/千克，每天的进货量p（千克）与销售价格x（元/千克）满足函数关系式 $\text{[math]}$ ，从市场反馈的信息发现，该海鲜食材每天的市场需求量q（千克）与销售价格x（元/千克）满足一次函数关系，部分数据如下表：

销售价格x（元/千克）

10

12

…

30

市场需求量q（千克）

30

28

…

10

（已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克）
1. （1）请写出q与x的函数关系式：；
2. （2）当每天的进货量小于或等于市场需求量时，这种海鲜食材能全部售出，而当每天的进货量大于市场需求量时，只能售出符合市场需求量的海鲜食材，剩余的海鲜食材由于保质期短而只能废弃.
  ①求出每天获得的利润y（元）与销售价格x的函数关系式；
  
  ②为了避免浪费，每天要确保这种海鲜食材能全部售出，求销售价格为多少元时，每天获得的利润（元）最大值是多少？
答案解析收藏纠错 + 选题
25. (2022九下·湖南期中) 如图，四边形ABCD内接于⊙O，对角线BD为⊙O直径，点E在BC延长线上，且∠E＝∠BAC.
1. （1）求证：DE是⊙O的切线；
2. （2）若AC $\text{[math]}$ DE，当AB＝16，DE＝4 $\text{[math]}$ 时，求⊙O半径的长.
答案解析收藏纠错 + 选题
26. (2022九下·湖南期中) 抛物线 $\text{[math]}$ 交x轴于点A，B（A在B的左边），交y轴于点C，顶点为M，对称轴MD交x轴于点D，E是线段MD上一动点，以OB，BE为邻边作平行四边形OBEF，EF交抛物线于点P，G（P在G的左边），交y轴于点H.
1. （1）求点A，B，C的坐标；
2. （2）如图1，当 $\text{[math]}$ 时，求DE的长；
3. （3）如图2，当 $\text{[math]}$ 时，
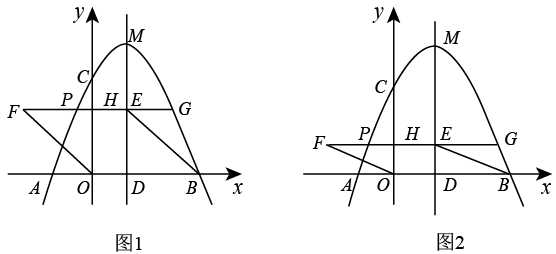
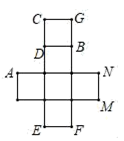
  ①求直线FC的解析式，并判断点M是否落在该直线上.
  ②连接CG，MG，CP，MP，记 $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ ▲ .
答案解析收藏纠错 + 选题