浙江省绍兴市嵊州市初级中学2020-2021学年八年级下学期...

更新时间：2022-05-07 浏览次数：86 类型：期中考试

一、单选题

1. (2021八下·嵊州期中) 下列图形中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024八下·德清期末) 要使二次根式 $\text{[math]}$ 有意义，则x的值可以为（）

A . $\text{[math]}$ B . 4 C . 2 D . 0

答案解析收藏纠错 + 选题
3. (2021八下·嵊州期中) 下列二次根式是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021八下·嵊州期中) 用配方法解方程 $\text{[math]}$ 时，配方结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·光明模拟) 用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应该假设这个三角形中（　　）

A . 有一个内角小于60° B . 每一个内角都小于60° C . 有一个内角大于60° D . 每一个内角都大于60°

答案解析收藏纠错 + 选题
6. (2021八下·嵊州期中) 已知关于X的方程x2 +bx+a=0有一个根是-a（a $\text{[math]}$ 0），则a-b的值为（）

A . 1 B . 2 C . -1 D . 0

答案解析收藏纠错 + 选题
7. 在某次演讲比赛中，五位评委给选手圆圆打分，得到互不相等的五个分数.若去掉一个最高分，平均分为x；去掉一个最低分，平均分为 $\text{[math]}$ ；同时去掉一个最高分和一个最低分，平均分为z，则 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·嵊州期中) 在探索数学名题“尺规三等分角”的过程中，有下面的问题：如图， $\text{[math]}$ 是平行四边形 $\text{[math]}$ 的对角线，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， ∠D=105°，则∠BAC的度数为（）

A . 24° B . 25° C . 26° D . 28°

答案解析收藏纠错 + 选题
9. (2022八下·章丘期末) 已知：四边形ABCD中，AB=2，CD=3，M、N分别是AD，BC的中点，则线段MN的取值范围是（）

A . 1＜MN＜5 B . 1＜MN≤5 C . $\text{[math]}$ ＜MN＜ $\text{[math]}$ D . $\text{[math]}$ ＜MN≤ $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

10. (2023八上·海淀期中) 若一个正多边形的每一个外角都等于 $\text{[math]}$ ，则这个正多边形的边数为．

答案解析收藏纠错 + 选题
11. (2021八下·嵊州期中) 今年3月12日，某学校开展植树活动，某植树小组20名同学的年龄情况如下表：
年龄（岁）
12
13
14
15
16
人数
1
4
3
5
7
则这20名同学年龄的众数和中位数分别是；.

答案解析收藏纠错 + 选题
12. (2021八下·嵊州期中) 已知菱形ABCD的对角线AC，BD交于点O，E为BC的中点，若OE＝3，则菱形的周长为.

答案解析收藏纠错 + 选题
13. (2021八下·嵊州期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ =.

答案解析收藏纠错 + 选题
14. (2023九上·永年期中) 某公司要招聘一名职员，根据实际需要，从学历、经验和工作态度三个方面对甲、乙两名应聘者进行了测试．测试成绩如下表所示．如果将学历、经验和工作态度三项得分按2：1：3的比例确定两人的最终得分，并以此为依据确定录用者，那么将被录用（填甲或乙）

应聘者

项目

甲

乙

学历

9

8

经验

7

6

工作态度

5

7

答案解析收藏纠错 + 选题
15. (2021八下·嵊州期中) 关于 x 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则常数k的取值范围是.

答案解析收藏纠错 + 选题
16. (2021八下·嵊州期中) 如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，下列五个结论：①EF=CF；②∠BAE+∠ECF=90°；③CF∥AE；④△ECF是等边三角形；⑤ $\text{[math]}$ ；其中一定成立的有（填序号）.

答案解析收藏纠错 + 选题

三、解答题

17. (2021八下·嵊州期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2021八下·嵊州期中) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题

四、题目

19. (2021八下·嵊州期中) 某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）.相关数据整理如下：
八年级抽取的学生的竞赛成绩：4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10.
七、八年级抽取的学生的竞赛成绩统计表

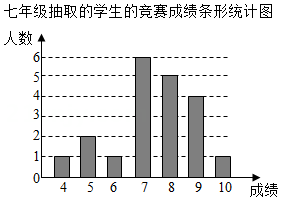
年级七年级八年级

平均数 7.4 7.4

中位数 a b

众数 7 c

合格率 85% 90%

根据以上值息，解答下列问题：
1. （1）填空a＝；b＝；c＝.
2. （2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；
3. （3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生整体成绩谁更优异.
答案解析收藏纠错 + 选题
20. (2021八下·嵊州期中) 如图，D，E分别是三角形ABC边AB，BC上的点，DE∥AC，点F在DE的延长线上，且∠DFC＝∠A.
1. （1）求证：四边形ADFC是平行四边形；
2. （2）若∠ACF比∠BDE大40°，求∠BDE的度数.
答案解析收藏纠错 + 选题
21. (2021八下·嵊州期中) 如图，在足够大的空地上有一段长为50米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏.
1. （1）若BC的长不小于20米，当所围成的矩形菜园的面积为1200平方米，求AB的长；
2. （2） ①所围成的矩形菜园的面积能否到达1300平方米？如果能，请求出AB的长；如果不能，请说明理由；
  ②设这个矩形菜园的面积为 $\text{[math]}$ ，利用配方法求这个矩形菜园的面积 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
22. (2021八下·嵊州期中) 方法回顾：在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：
第一步添加辅助线：如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF＝DE，连接CF；

第二步证明△ADE≌△CFE，再证四边形DBCF是平行四边形，从而得到DE∥BC，DE＝ $\text{[math]}$ BC.
1. （1）问题解决：
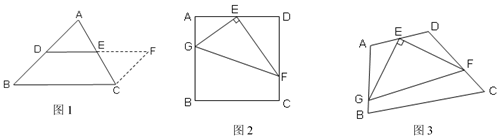
  如图2，在矩形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长.
2. （2）拓展研究：
  如图3，在四边形ABCD中，∠A＝105°，∠D＝120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝3，DF＝ $\text{[math]}$ ， ∠GEF＝90°，求GF的长.
答案解析收藏纠错 + 选题