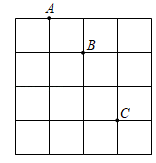
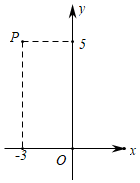

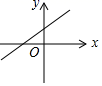 B .
B .  C .
C .  D .
D . 
①图象过点(0,﹣2)
②图象与x轴的交点是(﹣2,0)
③由图象可知y随x的增大而增大
④图象不经过第一象限
⑤图象是与y=﹣x+2平行的直线,
其中正确说法有( )
 B .
B . 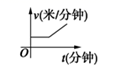 C .
C . 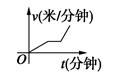 D .
D . 
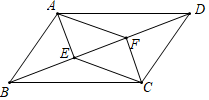
甲:只需要满足BE=DF
乙:只需要满足AE=CF
丙:只需要满足AE∥CF

数量x(个) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 8+0.2 | 16+0.2 | 24+0.2 | 32+0.2 | 40+0.2 |
根据表中提供的信息可知y与x之间的关系式是.



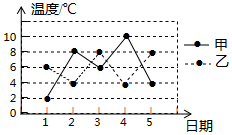
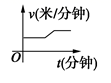
①在上升或下降过程中,无人机的速度是米/分;
②图中a表示的数是 , b表示的数是;
③无人机在60米高的上空停留的时间是分钟;
①若点P在第四象限,求m的取值范围;
②当点P到y轴的距离为3时,求点P的坐标.
| 组别 |
分数段 |
频数 |
频率 |
| 一 |
50.5~60.5 |
16 |
0.08 |
| 二 |
60.5~70.5 |
30 |
a |
| 三 |
70.5~80.5 |
50 |
0.25 |
| 四 |
80.5~90.5 |
b |
0.40 |
| 五 |
90.5~100.5 |
c |


甲店:购买电脑打八折;
乙店:先赠一台电脑,其余电脑打九折优惠.
设学校欲购置x台电脑,甲店购买费用为y甲(元),乙店购买费用为y乙(元).

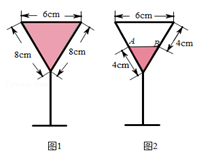
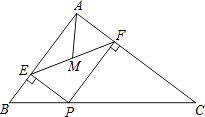
①线段AB和BD有何位置关系?请说明理由.
②若AB=2,BD=2AB时,求四边形GEHF的面积.
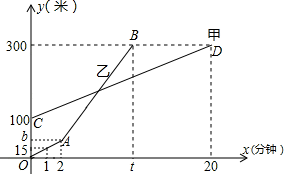
①则t= ▲ min;
②登山多长时间乙追上了甲,求出此时x的值;
③在上山过程中,先到达山顶的一人原地休息等待另一人,当甲、乙两人距地面高度差为50m时,求出此时x的值.