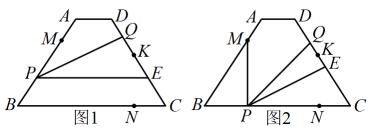 B .
B .  C .
C .  D .
D . 
|
如图,已知直线 请完成下面的说理过程. 解:已知 根据(内错角相等,两直线平行),得 再根据( ※ ),得 |
|

 B .
B .  C .
C .  D .
D . 
甲:只需要满足BE=DF
乙:只需要满足AE=CF
丙:只需要满足AE∥CF
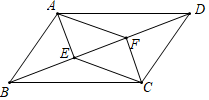
①两人行进的路程之和;
②当时,两人之间的距离;

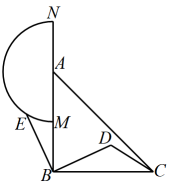
①当时,求线段
的长;
②若点M,N,E三点中,其中两点恰好关于第三点对称,直接写出此时m的值.