
 B .
B .  C .
C .  D .
D . 

 B .
B . 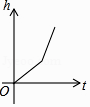 C .
C . 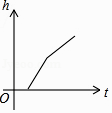 D .
D . 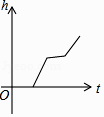

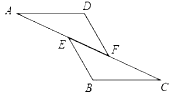



恰能判断的概率是.
分析:先将实际问题转化为数学问题,把超市看作一个点.
点到
,
两点的距离相等,根据性质: ▲ , 需用尺规作出 ▲ ;又点
到两相交直线
,
的距离相等,根据性质: ▲ , 需用尺规作出 ▲ ;而点
同时满足上述两个条件,因此应该是它们的交点.
请同学们先完成分析过程(即填空) ,再作图;


若
①当点在线段
上时(与点
不重合)我们可以大胆猜想
与
的数量关系是:
位置关系是:
请说明理由;
②当点在线段
的延长线上时,请在图②中画出相应的图形,并直接写出
与
的数量关系和位置关系;

如图③,若 , 点
在线段
上运动,请直接写出
与
的位置关系,并简要说明理由.

