辽宁省大连市甘井子区2020-2021学年七年级下学期期末数...

更新时间：2022-08-25 浏览次数：81 类型：期末考试

一、单选题

1. (2021七下·甘井子期末) 以下调查中，适合全面调查的是（）

A . 调查天和核心舱的设备零件的质量情况 B . 调查某池塘中现有鱼的数量 C . 调查市场上某种食品的色素含量是否符合国家标准 D . 调查春节联欢晚会的收视率

答案解析收藏纠错 + 选题
2. (2021七下·甘井子期末) 不等式2x+3≥7的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024七下·甘井子月考) 下列长度的三条线段能组成三角形的是（）

A . 3.6，3.6，7.2 B . 4，4，10 C . 5，6，10 D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021七下·甘井子期末) 在平面直角坐标系中，点A（1，1）经过平移后的对应点为B（3，4），下列平移正确的是（）

A . 先向右平移2个单位长度，再向下平移3个单位长度 B . 先向右平移2个单位长度，再向上平移3个单位长度 C . 先向左平移2个单位长度，再向下平移3个单位长度 D . 先向左平移2个单位长度，再向上平移3个单位长度

答案解析收藏纠错 + 选题
5. (2021七下·甘井子期末) 下列大小关系正确的是（）

A . $\text{[math]}$ 2＞0 B . 2 $\text{[math]}$ 3＜0 C . $\text{[math]}$ 1 D . 8 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021七下·甘井子期末) 为了解某班50名同学对电视节目的喜爱情况进行全面调查，并将调查到的数据绘制成如图所示的扇形统计图，其中A：新闻，B：体育，C：动画，D：娱乐，E：戏曲，则下列说法不正确的是（）

A . 喜爱新闻节目的有4人 B . 喜爱体育节目的占全班同学的10% C . 喜爱娱乐节目的有18人 D . 喜爱戏曲节目的占全班同学的6%

答案解析收藏纠错 + 选题
7. (2021七下·甘井子期末) 如图，两条直线a，b相交，若2∠3＝3∠1，则以下各角度数正确的是（）

A . ∠1＝72° B . ∠2＝120° C . ∠3＝144° D . ∠4＝36°

答案解析收藏纠错 + 选题
8. (2021七下·甘井子期末) 养牛场原有30头大牛和15头小牛，1天约用饲料675kg；一周后又购进20头大牛和35头小牛，这时1天约用饲料1250kg．求每头大牛和小牛1天各约用饲料多少千克？设每头大牛和小牛1天各约用饲料xkg和ykg，则可列二元一次方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021七下·甘井子期末) 如图，五边形ABCDE的内角都相等，且∠ADE＝∠DAE，∠BDC＝∠DBC，则∠ADB＝（）

A . 18° B . 36° C . 72° D . 108°

答案解析收藏纠错 + 选题
10. (2021七下·甘井子期末) 去年某市空气质量良好（二级以上）的天数与全年天数（365）之比达到60%，如果明年（365天）这样的比值要超过70%，那么明年空气质量良好的天数要比去年至少增加多少？设明年比去年空气质量良好的天数增加了x天，则可列一元一次不等式为（）

A . x+365×60%＞365×70% B . x+365×60%≥365×70% C . $\text{[math]}$ 365×70% D . $\text{[math]}$ 365×70%

答案解析收藏纠错 + 选题

二、填空题

11. (2022七下·广阳期中) 化简 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2021七下·甘井子期末) 为了解某校1500名学生的睡眠情况，随机抽取了150名学生作为样本进行调查，则抽取的样本容量是．

答案解析收藏纠错 + 选题
13. (2021七下·甘井子期末) 将一块直角三角尺ABC按如图所示的方式放置，其中点A、C分别落在直线a、b上，若a∥b，∠1＝62°，则∠2的度数为．

答案解析收藏纠错 + 选题
14. (2021七下·大连期末) 我国古代数学著作《九章算术》中记载：“今有大器五小器一容三斛，大器一小器五容二斛.问大小器各容几何.”其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，音hu ，是古代的一种容量单位）.1个大桶加上5个小桶可以盛酒2斛，问1个大桶、一个小桶分别可以盛酒多少斛？若设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据题意，可列方程组为.

答案解析收藏纠错 + 选题
15. (2021七下·甘井子期末) 若a＞b，则﹣3.5a+1 ﹣3.5b+1（填“＜”或“＞”）．

答案解析收藏纠错 + 选题
16. (2021七下·甘井子期末) 如图，在平面直角坐标系中，正方形OABC的四个顶点坐标分别是O（0，0），A（a² ， 0），B（n，n），C（0，b²），且|n|＝3，ab＞0，则a+b＝．

答案解析收藏纠错 + 选题

三、解答题

17. (2021七下·甘井子期末) 根据表回答问题：
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
17
$\text{[math]}$
256
259.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
285.61
289
1. （1） $\text{[math]}$ ； $\text{[math]}$ ．
2. （2） 272.25的平方根是；
3. （3）若a，b是表中两个相邻的数，a $\text{[math]}$ b，则a＝，b＝．
答案解析收藏纠错 + 选题
18. (2021七下·甘井子期末) 解下列方程组：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2021七下·甘井子期末) 解下列不等式（组）：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2021七下·甘井子期末) 某校为了增强学生垃圾分类的意识，举办了一次全校学生参与的有关垃圾分类的问卷测试（满分100分，得分均为整数），从中随机抽取部分学生的成绩，如图所示绘制了样本的频数分布表和频数分布直方图．
成绩x（分）
频数（人）
百分比
50≤x＜60
12
12%
60≤x＜70
20
a
70≤x＜80
b
c
80≤x＜90
28
28%
90≤x＜100
16
16%
请根据以上图表，回答下列问题：
1. （1）请直接写出a＝，b＝，c＝．
2. （2）补全频数分布直方图；
3. （3）若该校有学生1800人，成绩在80分以上为优秀，请你估计该校本次测试成绩优秀的学生有多少人？
答案解析收藏纠错 + 选题
21. (2021七下·甘井子期末) 如图，在△ABC中，CD是∠ACB的平分线，E、F分别在边AC，BC上，∠ADE＝∠B，∠DFC+∠ACB＝180°．求证：CD平分∠EDF．

答案解析收藏纠错 + 选题
22. (2021七下·甘井子期末) 某农场用2台大收割机和5台小收割机同时工作2小时共收割小麦3.6公顷，3台大收割机和2台小收割机同时工作5小时共收割小麦8公顷.1台大收割机和1台小收割机每小时各收割小麦多少公顷？

答案解析收藏纠错 + 选题
23. (2021七下·甘井子期末) 如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，
证明：∠BAC=∠B+2∠E

答案解析收藏纠错 + 选题
24. (2021七下·甘井子期末) 如图1，直线AD、BC相交于点O，∠DCP $\text{[math]}$ ∠BCP＝α，∠B＝3α．
1. （1）求证：AB∥CD；
2. （2）若∠D＝2∠DCP，求∠AOC的度数（用含α的式子表示）；
3. （3）如图2，若点M在线段AB上，连接OM，作∠OMB的平分线MN交CP于点N，若∠BCD＝n∠MNC，求 $\text{[math]}$ 的值（用含n的式子表示）．
答案解析收藏纠错 + 选题
25. (2021七下·甘井子期末) 某化工厂与A、B两地都分别有公路、铁路相连，从A地购买原料运回工厂制成产品运到B地销售．已知3t产品的销售款比4t原料的进货款多20000元，2t产品的销售款比1t原料的进货款多15000元．
1. （1）求每吨原料的进货款和产品的销售款分别多少元？
2. （2）如表为该化工厂与A、B两地的距离，已知公路运价为1.5元/（t•km），铁路运价为1.2元/（t•km），且这两次运输共支出公路运费15000元，铁路运费97200元，求这批原料比产品多多少吨？
  
  A地
  B地
  公路段路程（km）
  10
  20
  铁路段路程（km）
  120
  110
3. （3）工厂原计划从A地购买的原料和送往B地的产品一共20t，若要增加at的产品，就要再购买 $\text{[math]}$ at的原料，此时产品的销售款与原料的进货款之差不少于66000元，同时满足原料总重量是产品总重量的2倍，求至少需要再购买多少吨的原料？
答案解析收藏纠错 + 选题
26. (2021七下·甘井子期末) 定义：在平面直角坐标系中，对于点P（x，y），若点Q坐标为（2m﹣x，﹣y），其中m为常数，我们称点P与点Q是相关点．
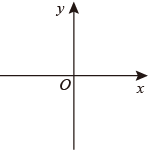
例如：当m＝0时，点P（1，2）的相关点Q为（﹣1，﹣2）．
1. （1）当m＝1时，点P坐标为（2，3），则它的相关点Q的坐标；
2. （2）若点P在y轴上，且它的相关点Q坐标为（m+2，﹣2m）．
  ①求△OPQ的面积；
  ②若存在一点A（x，6），使△APQ的面积大于△OPQ的面积，请直接写出x的取值范围 ▲ ；
3. （3）若点P（﹣m﹣3，4）和它的相关点Q到y轴的距离中最大值为m+8，求m的值．
答案解析收藏纠错 + 选题