重庆市江津区12校联盟学校2021-2022学年九年级下学期...

更新时间：2022-04-28 浏览次数：91 类型：期中考试

一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了A、B、C、D的四个答案，其中只有-一个是正确的，请在答题卡上正确答案所对应的框涂黑。

1. (2022九下·江津期中) -7的相反数是（）

A . -7 B . $\text{[math]}$ C . $\text{[math]}$ D . 7

答案解析收藏纠错 + 选题
2. (2022九下·江津期中) 下列图形既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022九下·江津期中) 下列计算正确的是（）

A . a³+a³=a⁶ B . a·a²=a³ C . （a²）³=a⁵ D . 3a-a=2

答案解析收藏纠错 + 选题
4. (2022九下·江津期中) 下列实数，介于5和6之间的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
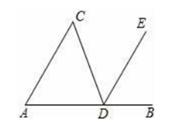
5. (2022九下·江津期中) 如图，点B是△ADC的边AD的延长线上一点，DE平分∠CDB，若∠C=50°，∠BDE=60°，则∠A的度数等于（）

A . 70° B . 100° C . 110° D . 120°

答案解析收藏纠错 + 选题
6. (2022九下·江津期中) 如图，扇形AOB的圆心角为124°，则∠ACB=（）

A . 114° B . 116° C . 118° D . 120°

答案解析收藏纠错 + 选题
7. (2022九下·江津期中) 如果 $\text{[math]}$ 是方程ax+（a- 2）y=0的一组解，则a的值（）

A . 1 B . -1 C . 2 D . -2

答案解析收藏纠错 + 选题
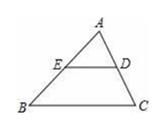
8. (2022九下·江津期中) 如图，△ABC中，E是AB的中点，过点E作ED∥BC，交AC于点D，则△AED与四边形BCDE的面积比是（）

A . 1：1 B . 1：2 C . 1：3 D . 1：4

答案解析收藏纠错 + 选题
9. (2022九下·江津期中) 下列图形都是由同样大小的矩形按一定的规律组成，其中，第①个图形中一共有6个矩形，第②个图形中一共有11个矩形，第③个图形中一共有16个矩形，……按此规律，第⑧个图形中矩形的个数为（）

A . 30 B . 36 C . 41 D . 45

答案解析收藏纠错 + 选题
10. (2022九下·江津期中) 如图是二次函数图象的y=ax²+bx+c一部分，图象过点A（-3，0），对称轴为直线x=-1。则以下结论错误的是（）

A . b²>4ac B . 2a+b=0 C . a+b+c=0 D . 5a<b

答案解析收藏纠错 + 选题
11. (2022九下·江津期中) 从-4，-3，1，3，4这五个数中，随机抽取一个数，记为m，若使得关于x，y的二元一次方程组 $\text{[math]}$ 有解，且使关于x的分式方程 $\text{[math]}$ 有正数解，那么这五个数中所有满足条件的m的值之和是（）

A . 1 B . 2 C . -1 D . -2

答案解析收藏纠错 + 选题
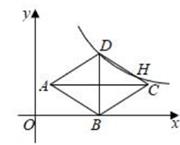
12. (2022九下·江津期中) 如图，在平面直角坐标系中，菱形ABCD的顶点B在x轴上，对角线BD平行于y轴，反比例函数y= $\text{[math]}$ （k>0，x>0）的图象经过点D，与CD边交于点H，若DH=2CH，菱形ABCD的面积为6，则k的值为（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题

二、填空题：（本大题4个小题，每小题4分，共16分）请将每小题的答案直接填在答题卡中对应的横线上。

13. (2022九下·江津期中) 计算：（π-1）⁰+ $\text{[math]}$ -（ $\text{[math]}$ ）²=

答案解析收藏纠错 + 选题
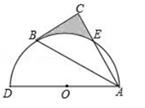
14. (2022九下·江津期中) 如图，以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点，交直角边AC于点E．B、E是半圆弧的三等分点，若AD=4，则图中阴影部分的面积为

答案解析收藏纠错 + 选题
15. (2022九下·江津期中) 从-3、-1、 $\text{[math]}$ 、1、3这五个数中，随机抽取一个数，记为a，则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为．

答案解析收藏纠错 + 选题
16. (2022九下·江津期中) 疫情隔离期间，为了降低外出感染风险，各大商超开通了送货到小区的便民服务，某商超推出适合大多数家庭需要的A、B、C三种蔬菜搭配装袋供市民直接选择．其中，甲种搭配每袋装有3千克A， 1千克B， 1千克C；乙种搭配每袋装有1千克A，2千克B，2千克C．甲、乙两种袋装蔬菜每袋成本价分别为袋中A、B、C三种蔬菜的成本价之和．已知A种蔬菜每千克成本价为2.4元，甲种搭配每袋售价为26元，利润率为30%，乙种搭配的利润率为20%．若这两种袋装蔬菜的销售利润率达到25%，则该商超销售甲、乙两种袋装蔬菜的数量之整数比是（商品的利润率= $\text{[math]}$ ×100%）

答案解析收藏纠错 + 选题

三、解答题：（本大题共2小题，每小题8分，共16分．）

17. (2022九下·江津期中) 如图，C，E，F，D共线，AB∥FD，BG∥FH，且AB=FD，BG=FH．求证：∠A=∠D．

答案解析收藏纠错 + 选题
18. (2022九下·江津期中) 为落实重庆市关于开展中小学课后服务工作的要求，某学校开展了四门校本课程供学生选择：A．趣味数学；B．博乐阅读；C．快乐英语；D．硬笔书法．全校共有100名学生选择了A课程，为了解选A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试．将他们的成绩（百分制）绘制成频数分布直方图．
1. （1）其中70≤x<80这一组的数据为74，73，72，75，76，76，79，则这组数据的中位数是，众数是
2. （2）根据题中信息，估计该校共有人，选A课程学生成绩在80≤x<90的有人．
3. （3）课程D在扇形统计图中所对应的圆心角的度数为
4. （4）如果学校规定每名学生要选两门不同的课程，小张和小王在选课程中，若第一次都选了课程C，那么他俩第二次同时选课程A或B的概率是多少？请用列表法或画树状图的方法加以说明．
答案解析收藏纠错 + 选题

四、解答题：（本大题共六个小题，19- -25 题每题10分，共70分）

19. (2022九下·江津期中)
1. （1）（a+b）（a-2b）-（a-b）²-b（a-b）．
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2022九下·江津期中)
如图，在平面直角坐标系中，O为原点，直线AB分别与x轴、y轴交于B和A，与反比例函数的图象交于C、D，CE⊥x轴于点E，tan∠ABO= $\text{[math]}$ ， OB=4，OE=2．
1. （1）求直线AB和反比例函数的解析式；
2. （2）求△OCD的面积．
答案解析收藏纠错 + 选题
21. (2022九下·江津期中) 随着柴静纪录片《穹顶之下》的播出，全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了A， B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元，用7500元购进A型空气净化器
和用6000元购进B型空气净化器的台数相同.
1. （1）求一台A型空气净化器和一台B型空气净化器的进价各为多少元？
2. （2）在销售过程中，A型空气净化器因为净化能力强，嗓音小而更受消费者的欢迎．为了增大B型空气净化器的销量，商社电器决定对B型空气净化器进行降价销售，经市场调查，当B型空气净化器的售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台．如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为多少元？
答案解析收藏纠错 + 选题
22. (2022九下·江津期中) 如图，某建筑物BC上有一旗杆AB，小明在F处，由E点观察到旗杆顶部A的仰角为52°，底部B的仰角为45°，小明的观测点与地面距离EF为1.6m，
1. （1）若F与BC相距12m，求建筑物BC的高度；
2. （2）若旗杆AB长3.15m，求建筑物BC的高度．（结果精确到0.1m）（参考数据： $\text{[math]}$ ≈1.414，sin52°≈0.788，tan52°≈1.280）．
答案解析收藏纠错 + 选题
23. (2022九下·江津期中) 有一个n位自然数 $\text{[math]}$ 能被x₀整除，依次轮换个位数字得到的新数 $\text{[math]}$ 能被x₀+1整除，再依次轮换个位数字得到的新数 $\text{[math]}$ 能被x₀+2整除，按此规律轮换后， $\text{[math]}$ 能被x₀+3整除，……， $\text{[math]}$ 能被x₀+n-1整除，则称这个n位数 $\text{[math]}$ 是x₀的一个“轮换数”。例如：60能被5整除，06能被6整除，则称两位数60是5的一个“轮换数”；再如：324能被2整除，243能被3整除，432能被4整除，则称三位数324是2个一个“轮换数”．
1. （1）若一个两位自然数的个位数字是十位数字的2倍，求证这个两位自然数一定是“轮换数”．
2. （2）若三位自然数 $\text{[math]}$ 是3的一个“轮换数”，其中a=2，求这个三位自然数 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2022九下·江津期中) 如图，正方形ABCD的边长为6，点E在边AB上，连接ED，过点D作FD⊥DE与BC的延长线相交于点F，连接EF与边CD相交于点G、与对角线BD相交于点H．
1. （1）若BD=BF，求BE的长；
2. （2）若∠2=2∠1，求证：HF=HE+HD．
答案解析收藏纠错 + 选题
25. (2022九下·江津期中) 如图1，已知抛物线y= $\text{[math]}$ 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D是点C关于抛物线对称轴的对称点，连接CD，过点D作DH⊥x轴于点H，过点A作AE⊥AC交DH的延长线于点E．
1. （1）求线段DE的长度；
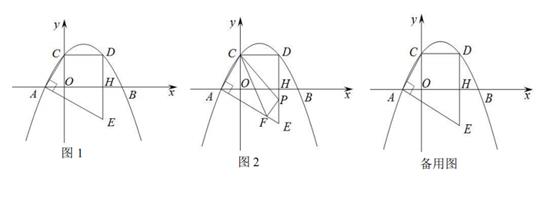
2. （2）如图2，试在线段AE上找一点F，在线段上找一点P，且点为直线PF上方抛物线上的-点，求当△CPF的周长最小时，△MPF面积的最大值是多少；
3. （3）在（2）问的条件下，将得到的△CFP沿直线AE平移得到，将△C'F'P'沿C'P'翻折得到△C'P'F"，记在平移过称中，直线F'P'与x轴交于点K，当NF'F"K为等腰三角形，直接写出OK的值．
答案解析收藏纠错 + 选题