江苏省宿迁泗洪县2022年九年级数学一模模拟试卷

更新时间：2024-07-13 浏览次数：76 类型：中考模拟

一、单选题

1. (2024八下·广饶期末) 一元二次方程2x²＋6x＋3＝ 0 经过配方后可变形为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·泗洪模拟) 已知 $\text{[math]}$ 的内心为P，则下列说法错误的是（）

A . $\text{[math]}$ B . P在 $\text{[math]}$ 的内部 C . P为 $\text{[math]}$ 三个内角平分线的交点 D . P到三边距离相等

答案解析收藏纠错 + 选题
3. (2022·泗洪模拟) 如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·泗洪模拟) 若一个圆锥的侧面展开图是半径为 $\text{[math]}$ 、圆心角为 $\text{[math]}$ 的扇形，则这个圆锥的底面半径长是（）

A . 6cm B . 9cm C . 12cm D . 18cm

答案解析收藏纠错 + 选题
5. (2022·泗洪模拟) 把1双白手套和1双黑手套1只1只的扔进抽屉里，黑暗中摸出2只，恰好成1双的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·泗洪模拟) 下列函数属于二次函数的是（　　）

A . y＝x﹣ $\text{[math]}$ B . y＝（x﹣3）²﹣x² C . y＝ $\text{[math]}$ ﹣x D . y＝2（x+1）²﹣1

答案解析收藏纠错 + 选题

7. (2022·泗洪模拟) 二次函数y＝ax²＋bx＋c的图象上部分点的坐标（x，y）对应值列表如下：

x	…	﹣3	﹣2	﹣1	0	1	…
y	…	﹣3	﹣2	﹣3	﹣6	﹣11	…

则关于该二次函数的图象与性质，下列说法正确的是（）

A . 开口方向向上 B . 当x＞﹣2时，y随x增大而增大 C . 函数图象与x轴没有交点 D . 函数有最小值是﹣2

答案解析收藏纠错 + 选题

8. (2024九上·汉川月考) 关于x的二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，函数有最小值4，则h的值为（）

A . 0或2 B . 2或4 C . 0或4 D . 0或2或4

答案解析收藏纠错 + 选题

二、填空题

9. (2022·泗洪模拟) 若抛物线 $\text{[math]}$ 与x轴没有交点，则m的取值范围是.

答案解析收藏纠错 + 选题
10. (2022·泗洪模拟) 设 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
11. (2022·泗洪模拟) 已知 $\text{[math]}$ 的直径为10cm， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的两条弦，AB $\text{[math]}$ CD， $\text{[math]}$ ， $\text{[math]}$ ，则弦 $\text{[math]}$ 和 $\text{[math]}$ 之间的距离是cm

答案解析收藏纠错 + 选题
12. (2022·泗洪模拟) 如图，已知圆锥的底面半径为3，高为4，则该圆锥的侧面积为．

答案解析收藏纠错 + 选题
13. (2022·泗洪模拟) 已知一组数据的方差S²＝ $\text{[math]}$ [（6﹣10）²+（9﹣10）²+（a﹣10）²+（11﹣10）²+（b﹣10）²]＝6.8，则a²+b²的值为.

答案解析收藏纠错 + 选题
14. (2022·泗洪模拟) 若a、b、c的方差为3，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的方差为.

答案解析收藏纠错 + 选题
15. (2022·泗洪模拟) 已知函数 $\text{[math]}$ 与x轴的交点为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2022九上·仙居月考) 已知函数y＝|x²﹣4|的大致图象如图所示，那么：方程|x²﹣4|＝m ．（m为实数）
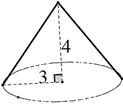
①若该方程恰有3个不相等的实数根，则m的值是．

②若该方程恰有2个不相等的实数根，则m的取值范围是．

答案解析收藏纠错 + 选题
17. (2022·泗洪模拟) 已知关于x的一元二次方程 $\text{[math]}$ ＝ $\text{[math]}$ 、h，k均为常数且 $\text{[math]}$ 的解是 $\text{[math]}$ ＝ $\text{[math]}$ ， $\text{[math]}$ ＝ $\text{[math]}$ ，则方程 $\text{[math]}$ 的解是.

答案解析收藏纠错 + 选题

三、解答题

18. (2022·泗洪模拟) 如图，AB是⊙O的直径，弦CD⊥AB于E，∠CDB＝30°，CD＝ $\text{[math]}$ ，求阴影部分的面积．

答案解析收藏纠错 + 选题
19. (2022·泗洪模拟) 如果关于x的一元二次方程ax²＋bx＋c＝0（a≠0）有两个实数根，且其中一个根比另一个根大1，那么称这样的方程为“邻根方程”.例如，一元二次方程x²＋x＝0的两个根是x₁＝0，x₂＝﹣1，则方程x²＋x＝0是“邻根方程”.
1. （1）通过计算，判断方程x²﹣5x＋6＝0是否是“邻根方程”；
2. （2）已知关于x的方程x²﹣（m﹣1）x﹣m＝0（m是常数）是“邻根方程”，求m的值.
答案解析收藏纠错 + 选题
20. (2022·泗洪模拟) 已知：x₁、x₂是关于x的方程x²+（2a﹣1）x+a²=0的两个实数根且（x₁+2）（x₂+2）=11，求a的值．

答案解析收藏纠错 + 选题
21. (2022·泗洪模拟) 在 $\text{[math]}$ 年“新技术支持未来教育”的教师培训活动中，会议就“面向未来的学校教育、家庭教育及实践应用演示”等问题进行了互动交流，记者随机采访了部分参会教师，对他们发言的次数进行了统计，并绘制了不完整的统计表和条形统计图.
组别
发言次数n
百分比
A
0≤n＜3
10%
B
3≤n＜6
20%
C
6≤n＜9
25%
D
9≤n＜12
30%
E
12≤n＜15
10%
F
15≤n＜18
m%
请你根据所给的相关信息，解答下列问题：
1. （1）本次共随机采访了名教师，m=.
2. （2）补全条形统计图；
3. （3）已知受访的教师中，E组只有2名女教师，F组恰有1名男教师，现要从E组、F组中分别选派1名教师写总结报告，请用列表法或画树状图的方法，求所选派的两名教师恰好是1男1女的概率.
答案解析收藏纠错 + 选题
22. (2022·泗洪模拟) 某商品现在的售价为每件 $\text{[math]}$ 元，每星期可卖出 $\text{[math]}$ 件，市场调查反映：售价每上涨 $\text{[math]}$ 元，每星期要少卖出 $\text{[math]}$ 件，已知商品的进价为每件 $\text{[math]}$ 元，设销售单价为每件x元 $\text{[math]}$ ，每星期的销售量为y件.
1. （1）写出y与x的函数解析式，并直接写出x的取值范围；
2. （2）商店要使每星期销售利润为 $\text{[math]}$ 元，销售价应为每件多少元？
3. （3）当销售价定为每件多少元时，每星期获得利润最大？最大利润为多少元？
答案解析收藏纠错 + 选题
23. (2022·泗洪模拟) 如图，二次函数y₁＝﹣ $\text{[math]}$ x²+bx+c的图象与x轴、y轴分别交于点A（﹣1，0）和点B（0，2），图象的对称轴交x轴于点C，一次函数y₂＝mx+n的图象经过点B、C.
1. （1）求二次函数的解析式y₁和一次函数的解析式y₂；
2. （2）点P在x轴下方的二次函数图象上，且S_△ACP＝33，求点P的坐标；
3. （3）结合图象，求当x取什么范围的值时，有y₁≤y₂.
答案解析收藏纠错 + 选题
24. (2022·泗洪模拟) 在平面直角坐标系中，已知抛物线经过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点．
1. （1）求抛物线的解析式；
2. （2）若点 $\text{[math]}$ 为第三象限内抛物线上一动点，点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数关系式，并求出 $\text{[math]}$ 的最大值．
3. （3）若点 $\text{[math]}$ 是抛物线上的动点，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的动点，若以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形为平行四边形，直接写出相应的点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
25. (2022·泗洪模拟) 某园林专业户王先生计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润 $\text{[math]}$ 与投资量x成正比例关系，如图1所示；种植花卉的利润 $\text{[math]}$ 与投资量x成二次函数关系，如图2所示（图中实线部分）
1. （1）分别求出 $\text{[math]}$ 与 $\text{[math]}$ 关于投资量x的函数解析式；
2. （2）王先生以总资金 $\text{[math]}$ 万元投入种植花卉和树木，且投入种植花卉的资金不能超过投入种植树木资金的 $\text{[math]}$ 倍.设王先生投入种植花卉资金m万元，种植花卉和树木共获利W万元，求W关于m的函数解析式，并求他至少获得多少利润？他能获取的最大利润是多少？
3. （3）若王先生想获利不低于 $\text{[math]}$ 万，在（ $\text{[math]}$ ）的条件下，直接写出投资种植花卉的资金m的范围.
答案解析收藏纠错 + 选题
26. (2022·南城模拟) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于点A、B，与y轴交于点C，连接BC， $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，点D为此抛物线的顶点.
1. （1）求抛物线的解析式；
2. （2）点E是第一象限内抛物线上的动点，连接BE和CE，求 $\text{[math]}$ 面积的最大值；
3. （3）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标.
答案解析收藏纠错 + 选题