![]()
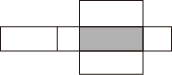 B .
B . 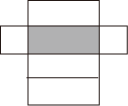 C .
C . 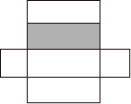 D .
D . 
 B .
B .  C .
C .  D .
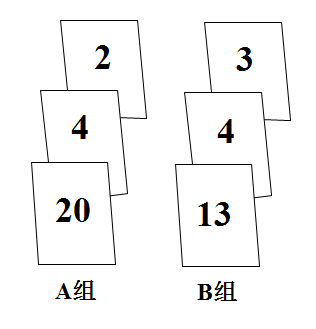
D . 
①是等腰三角形②
③四边形
是平行四边形,周长是14cm④动点
无论移动到OA上哪一点(P不与O、A重合),
的值为固定值是
.

选择各兴趣社团的人数统计表:
兴趣社团 | 人数 |
A.篮球社团 | 10 |
B.书香社团 | 8 |
C.舞蹈社团 | a |
D.编程社团 | 4 |
E.合唱社团 | 6 |
选择各兴趣社团的人数统计图:
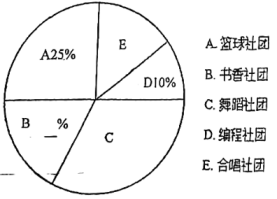
根据以上信息:


【问题探究】为解决上面的数学问题,我们可以运用数形结合的思想方法,借助图1所示的三角形,把数量关系和几何图形巧妙地结合起来进行探究.图1中,

第1行圆圈中的数为1,即;
第2行两个圆圈中数的和为2+2=2×2,
即;
第3行三个圆圈中数的和为3+3+3=3×3
即;
……;
第行
个圆圈中数的和为
, 即
.所有圆圈中数的和为
.
要解决上面的问题,我们不妨先从特例入手:
探究一:计算.

将图2按逆时针方向两次旋转得到图3、图4.观察这三个图形,可以发现同一位置圆圈的数字之和都是5(如图5),而图5共有(1+2)个这样的圆圈,因此图5中所有数字之和为5×(1+2).则图2中所有数字之和为 , 所以得到等式
.

仿照上述方法,将图6按逆时针方向两次旋转得到图7、图8.观察这三个图形,可以发现同一位置圆圈的数字之和都是(如图9),而图9共有个这样的圆圈,因此图9中所有数字之和为.那么图6中所有数字之和为,所以得到等式.(仿照上述方法,写出探究得出的式子).
计算:.(直接写出结果)
