

 B .
B .  C .
C .  D .
D . 




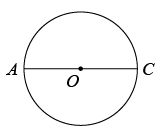
已知:如图, .
求作:矩形 ,使矩形
内接于
,对角线
与
的夹角为
作法:①作 的直径
;
②以点A为圆心, 长为半径作弧.交直线
上方的圆于点B;
③连接 并延长交
于点D;
④顺次连接 、
、
和
.
四边形 就是所求作的矩形,
根据小明设计的尺规作图过程
证明:∵点A,C都在 上,
,
.
∴四边形 是平行四边形.( )(填推理依据).
又 是
的直径,
( )(填推理依据).
∴四边形 是矩形.
又 ▲ .
是等边三角形.
∴四边形 是所求作的矩形.

①若m=2,求这个一次函数的解析式;
②若当x 3时,不等式mx﹣1
ax+b始终成立,结合函数图象,直接写出m的取值范围.
|
d(米) |
0 |
| 1 | 2.0 | 3 | | … |
| h(米) | | 1.6 | 2.1 | 2.5 | 2.1 | 0 | … |

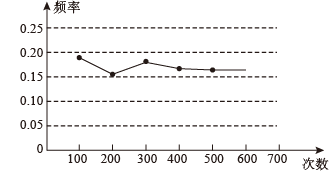
a.1月31日至2月20日观影人数统计图:

b.1月31日至2月20日观影人频数统计图:

c.1月31日至2月20日观影人数在 的数据为t
91,92,93,93,95,98,99
根据以上信息,回答下列问题:
②请用等式写出 与
的数量关系,并证明.
①如果点 的2倍关联点M在x轴上,那么点M的坐标是;
②如果点 是点
的k倍关联点,且满足
,
.那么k的最大值为;