北京市房山区2022年九年级中考二模数学试题

更新时间：2024-07-13 浏览次数：167 类型：中考模拟

一、单选题

1. (2024七上·讷河期末) 如图是某个几何体的平面展开图，该几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022·房山模拟) 在疫情防控的特殊时期，为了满足初三高三学生的复习备考需求，北京市教委联合北京卫视共同推出电视课堂节目《老师请回答特别节目“空中课堂”》，在节目播出期间．全市约有200000名师生收看了节目．将200000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·房山模拟) 2022年北京和张家口成功举办了第24届冬奥会和冬残奥会．下面关于奥运会的剪纸图片中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·房山模拟) 如图，直线 $\text{[math]}$ ，直线 $\text{[math]}$ 分别与直线 $\text{[math]}$ 交于点E，F，点G在直线 $\text{[math]}$ 上， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·房山模拟) 如图，实数a ， b在数轴上的对应点的位置如图所示，则正确的结论是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八上·雨花开学考) 《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架，其中《盈不足》卷记载了一道有趣的数学问题：“今有共买物，人出八，赢三；人出七，不足四，问人数、物价各几何？”译文：“今有人合伙购物，每人出8钱，会多出3钱；每人出7钱，又差4钱，问人数，物价各多少？”设人数为x人，物价为y钱，根据题意，下面所列方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·房山模拟) 如果甲、乙、丙三位同学随机站成一排，那么甲站在中间的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·房山模拟) 图，在平面直角坐标系 $\text{[math]}$ 中，点A的坐标是 $\text{[math]}$ ，点B是函数 $\text{[math]}$ 图象上的一个动点，过点B作 $\text{[math]}$ 轴交函数 $\text{[math]}$ 的图象于点C，点D在x轴上（D在A的左侧，且 $\text{[math]}$ ，连接 $\text{[math]}$ ．有如下四个结论：①四边形 $\text{[math]}$ 可能是菱形；②四边形 $\text{[math]}$ 可能是正方形；③四边形 $\text{[math]}$ 的周长是定值；④四边形 $\text{[math]}$ 的面积是定值．所有正确结论的序号是（）

A . ①② B . ②③ C . ③④ D . ①④

答案解析收藏纠错 + 选题

二、填空题

9. (2022·房山模拟) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是．

答案解析收藏纠错 + 选题
10. (2024九上·深圳开学考) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2022·房山模拟) 方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
12. (2022·房山模拟) 若已知关于x的一元二次方程 $\text{[math]}$ 总有两个不相等的实数根，则的取值范围为．

答案解析收藏纠错 + 选题
13. (2022·房山模拟) 如图，双曲线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于A，B两点，若点A的坐标为 $\text{[math]}$ ，则点B的坐标为．

答案解析收藏纠错 + 选题
14. (2022·房山模拟) 下列说法正确的是．
（1）一组数据：1，2，2，3，若再添加一个数据2，则平均数和方差均不发生变化；
（2）已知 $\text{[math]}$ ．若n为整数，且 $\text{[math]}$ ，则n的值为44；
（3）如图是小明某一天测得的7次体温情况的折线统计图，这组数据的中位数是36.6．

答案解析收藏纠错 + 选题
15. (2022·房山模拟) 如图，点P在直线 $\text{[math]}$ 外，点A、B、C、D均在直线 $\text{[math]}$ 上，如果 $\text{[math]}$ ，只需添加一个条件即可证明 $\text{[math]}$ ，这个条件可以是（写出一个即可）．

答案解析收藏纠错 + 选题

三、解答题

16. (2022·房山模拟) 为确定传染病的感染者，医学上可采用“二分检测方案”．假设待检测的总人数是 $\text{[math]}$ （ $\text{[math]}$ 为正整数）．将这 $\text{[math]}$ 个人的样本混合在一起做第1轮检测（检测1次），如果检测结果是阴性，可确定这些人都未感染；如果检测结果是阳性，可确实其中感染者，则将这些人平均分成两组，每组 $\text{[math]}$ 个人的样本混合在一起做第2轮检测，每组检测1次．依此类推：每轮检测后，排除结果为阴性的组，而将每个结果为阳性的组再平均分成两组，做下轮检测，直至确定所有的感染者．
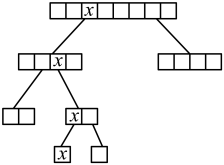
例如，当待检测的总人数为8，且标记为“ $\text{[math]}$ ”的人是唯一感染者时，“二分检测方案”可用如图所示．从图中可以看出，需要经过4轮共 $\text{[math]}$ 次检测后，才能确定标记为“ $\text{[math]}$ ”的人是唯一感染者．
1. （1） n的值为；
2. （2）若待检测的总人数为8，采用“二分检测方案”，经过4轮共9次检测后确定了所有的感染者，写出感染者人数的所有可能值；
答案解析收藏纠错 + 选题
17. (2022·房山模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022·房山模拟) 解不等式组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2022·房山模拟) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
20. (2022·房山模拟) 下面是小文设计的“过圆外一点作圆的切线”的作图过程．
已知： $\text{[math]}$ 和圆外一点P．
求作：过点P的 $\text{[math]}$ 的切线．
作法：①连接 $\text{[math]}$ ；作 $\text{[math]}$ 的垂直平分线与 $\text{[math]}$ 交于点M；②以 $\text{[math]}$ 半径作 $\text{[math]}$ ，交 $\text{[math]}$ 于点A，B；③作直线 $\text{[math]}$ ；
所以直线 $\text{[math]}$ 为 $\text{[math]}$ 的切线．
请利用尺规作图补全小文的作图过程，并完成下面的证明．
证明：连接 $\text{[math]}$ ．
∵ $\text{[math]}$ 为 $\text{[math]}$ 的直径，
∴ $\text{[math]}$ ▲ = ▲ $\text{[math]}$ （）（填推理的依据）．
∴ $\text{[math]}$
∵ $\text{[math]}$ 为 $\text{[math]}$ 半径，
∴直线 $\text{[math]}$ 为 $\text{[math]}$ 的切线．（）（填推理的依据）．

答案解析收藏纠错 + 选题
21. (2022·房山模拟) 如图，在▱ABCD中，AC ， BD交于点O ，且AO＝BO ．
1. （1）求证：四边形ABCD是矩形；
2. （2） ∠ADB的角平分线DE交AB于点E ，当AD＝3，tan∠CAB＝ $\text{[math]}$ 时，求AE的长．
答案解析收藏纠错 + 选题
22. (2022·房山模拟) 在平面直角坐标系 $\text{[math]}$ 中，函数 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，
1. （1）当点 $\text{[math]}$ 的横坐标为1时，求此时 $\text{[math]}$ 的值；
2. （2）横、纵坐标都是整数的点叫做整点．记函数 $\text{[math]}$ 的图像在点 $\text{[math]}$ 之间的部分与线段 $\text{[math]}$ 围成的区域（不含边界）为 $\text{[math]}$ ，
  ①当 $\text{[math]}$ 时，结合函数图象，求区域 $\text{[math]}$ 内整点的个数；
  ②若区域 $\text{[math]}$ 内恰有1个整点，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
23. (2022·房山模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点E，过点E作直线 $\text{[math]}$ 的垂线于交 $\text{[math]}$ 于点F， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）过点E作 $\text{[math]}$ 于点H，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
24. (2022·房山模拟) 某学校初二和初三两个年级各有600名同学，为了科普卫生防疫知识，学校组织了一次在线知识竞赛，小宇分别从初二、初三两个年级随机抽取了40名同学的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．
a．初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下（数据分成5组： $\text{[math]}$ ）：
b．初二年级学生知识竞赛成绩在 $\text{[math]}$ 这一组的数据如下：
80 80 81 83 83 84 84 85 86 87 88 89 89
c．初二、初三学生知识竞赛成绩的平均数、中位数、方差如下：

平均数
中位数
方差
初二年级
80.8
m
96.9
初三年级
80.6
86
153.3
根据以上信息，回答下列问题：
1. （1）补全上面的知识竞赛成绩频数分布直方图；
2. （2）写出表中m的值；
3. （3） A同学看到上述的信息后，说自己的成绩能在本年级排在前40%，B同学看到A同学的成绩后说：“很遗憾，你的成绩在我们年级进不了前50%”，请判断A同学是（填“初二”或“初三”）年级的学生，你判断的理由是．
答案解析收藏纠错 + 选题

25. (2022·房山模拟) 如图，点C是以点O为圆心，AB为直径的半圆上的动点（不与点A ， B重合），AB＝6cm ，过点C作CD⊥AB于点D ， E是CD的中点，连接AE并延长交 $\text{[math]}$ 于点F ，连接FD ．小腾根据学习函数的经验，对线段AC ， CD ， FD的长度之间的关系进行了探究．

下面是小腾的探究过程，请补充完整：

（1）对于点C在 $\text{[math]}$ 上的不同位置，画图、测量，得到了线段AC ， CD ， FD的长度的几组值，如表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7	位置8
AC/cm	0.1	0.5	1.0	1.9	2.6	3.2	4.2	4.9
CD/cm	0.1	0.5	1.0	1.8	2.2	2.5	2.3	1.0
FD/cm	0.2	1.0	1.8	2.8	3.0	2.7	1.8	0.5

在AC ， CD ， FD的长度这三个量中，确定的长度是自变量，的长度和的长度都是这个自变量的函数；

（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解答问题：当CD＞DF时，AC的长度的取值范围是．

答案解析收藏纠错 + 选题

26. (2022·房山模拟) 已知二次函数 $\text{[math]}$ ．
1. （1）二次函数图象的对称轴是直线 $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，y的最大值与最小值的差为9，求该二次函数的表达式；
3. （3）若 $\text{[math]}$ ，对于二次函数图象上的两点 $\text{[math]}$ ，当 $\text{[math]}$ 时，均满足 $\text{[math]}$ ，请结合函数图象，直接写出t的取值范围．
答案解析收藏纠错 + 选题
27. (2022·房山模拟) 如图，点P是正方形 $\text{[math]}$ 内一动点，满足 $\text{[math]}$ 且 $\text{[math]}$ ，过点D作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点E．
1. （1）依题意补全图形；
2. （2）用等式表示线段 $\text{[math]}$ 之间的数量关系，并证明；
3. （3）连接 $\text{[math]}$ ，若 $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 长度的最小值．
答案解析收藏纠错 + 选题
28. (2022·房山模拟) 对于平面直角坐标系 $\text{[math]}$ 中的图形 $\text{[math]}$ 和图形 $\text{[math]}$ ．给出如下定义：在图形 $\text{[math]}$ 上存在两点A，B（点A，B可以重合），在图形 $\text{[math]}$ 上存在两点M，N，（点M、N可以重合）使得 $\text{[math]}$ ，则称图形 $\text{[math]}$ 和图形 $\text{[math]}$ 满足限距关系
1. （1）如图1，点 $\text{[math]}$ ，点P在线段 $\text{[math]}$ 上运动（点P可以与点C，E重合），连接 $\text{[math]}$ ．
  ①线段 $\text{[math]}$ 的最小值为，最大值为；线段 $\text{[math]}$ 的取值范围是；
  ②在点O，点D中，点与线段 $\text{[math]}$ 满足限距关系；
2. （2）在（1）的条件下，如图2， $\text{[math]}$ 的半径为1，线段 $\text{[math]}$ 与x轴、y轴正半轴分别交于点F，G，且 $\text{[math]}$ ，若线段 $\text{[math]}$ 与 $\text{[math]}$ 满足限距关系，求点F横坐标的取值范围；
3. （3） $\text{[math]}$ 的半径为 $\text{[math]}$ ，点H，K是 $\text{[math]}$ 上的两个点，分别以H，K为圆心，2为半径作圆得到 $\text{[math]}$ 和 $\text{[math]}$ ，若对于任意点H，K， $\text{[math]}$ 和 $\text{[math]}$ 都满足限距关系，直接写出r的取值范围．
答案解析收藏纠错 + 选题