
 D .
D . 
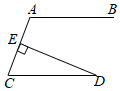
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 


施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
累计完成施工量/米 | 25 | 50 | 75 | 100 | 115 | 155 | 195 | 235 | 275 | 315 |
甲队技术改进后比技术改进前每天多修路米.


61,74,68,62,73,70,72,78,69,74,79,68,74.
|
竞赛成绩分组统计表 |
||
|
组别 |
竞赛成绩分组 |
频数 |
|
1 |
60 |
a |
|
2 |
70 |
b |
|
3 |
80 |
12 |
|
4 |
90 |
d |
竞赛成绩扇形统计图

请根据以上信息,解答下列问题:


备用图


