![]()
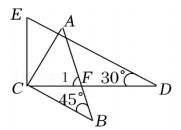
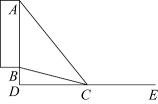
 B .
B . 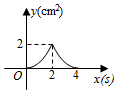 C .
C .  D .
D . 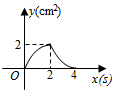
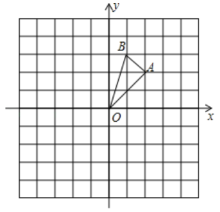
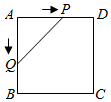
⑴画出 , 直接写出点
,
的坐标;
⑵计算在旋转过程中,所扫过的面积.
⑶以原点为位似中心,位似比为2,在第三象限画出
放大后的
.

甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
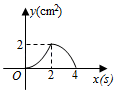
②当时,
(用含
的代数式表示);
①已知 , 求
的值;
②证明: .