山东省青岛西海岸新区2022年九年级二模数学试题

更新时间：2022-06-14 浏览次数：102 类型：中考模拟

一、单选题

1. (2022七上·韶关期中) $\text{[math]}$ 的倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·青岛模拟) “中国结”是我国特有的手工编织工艺品，也是一种传统吉祥装饰物．下列四个中国结图案中，既是中心对称图形又是轴对称图形的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2022·七星关模拟) 《2021—2022中国大数据产业发展报告》预测，未来三年，我国大数据产业市场将保持12%以上的增速，到2023年整体规模将达到11522.5亿元.11522.5亿用科学记数法可以表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·青岛模拟) 当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·青岛模拟) 如图，线段 $\text{[math]}$ 经过平移得到线段 $\text{[math]}$ ，其中点 $\text{[math]}$ ， $\text{[math]}$ 的对应点分别为点 $\text{[math]}$ ， $\text{[math]}$ ，这四个点都在格点上．若线段 $\text{[math]}$ 上有一个点 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ，则点 $\text{[math]}$ 在 $\text{[math]}$ 上的对应点 $\text{[math]}$ 的坐标为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·青岛模拟) 如图 $\text{[math]}$ 是 $\text{[math]}$ 切线，点A为切点， $\text{[math]}$ 交 $\text{[math]}$ 于点C，点D在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·青岛模拟) 在平面直角坐标系中， $\text{[math]}$ 为坐标原点，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，若 $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，且使得 $\text{[math]}$ 为等腰三角形，则满足条件的点 $\text{[math]}$ 有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

8. (2022·青岛模拟) 二次函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是常数， $\text{[math]}$ ）的自变量 $\text{[math]}$ 与函数值 $\text{[math]}$ 的部分对应值如下表：

$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	0	1	2	…
$\text{[math]}$	…	$\text{[math]}$	2	1	2	$\text{[math]}$	$\text{[math]}$	…

下列说法错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 和2是方程 $\text{[math]}$ 的两个根 C . $\text{[math]}$ D . 二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴无交点

答案解析收藏纠错 + 选题

二、填空题

9. (2022·青岛模拟) 不等式组 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
10. (2022·青岛模拟) 甲，乙两人进行掷飞镖比赛，每人各掷6次，所得环数的平均数相同．甲所得环数为：9，8，9，6，10，6，乙所得环数的方差为4，那么成绩较为稳定的是．（填“甲”或“乙”）

答案解析收藏纠错 + 选题
11. (2022·青岛模拟) 扶贫工作小组对果农进行精准扶贫，帮助果农将一种有机生态水果拓宽了市场．与去年相比，今年这种水果的产量增加了1000千克，每千克的平均批发价比去年降低了1元，批发销售总额比去年增加了20%．已知去年这种水果批发销售总额为10000元，则这种水果今年每千克的平均批发价是元．

答案解析收藏纠错 + 选题
12. (2023·榕城模拟) 往直径为 $\text{[math]}$ 的圆柱形容器内装入一些水以后，截面如图，若水面宽 $\text{[math]}$ ，则水的最大深度为cm．

答案解析收藏纠错 + 选题
13. (2022·青岛模拟) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，菱形的一个顶点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2022·青岛模拟) 如图是一张矩形纸片 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，把 $\text{[math]}$ 沿直线 $\text{[math]}$ 对折，使点 $\text{[math]}$ 落在对角线 $\text{[math]}$ 上的点 $\text{[math]}$ 处，连接 $\text{[math]}$ ．若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

15. (2022·青岛模拟) 求作 $\text{[math]}$ 的内切圆 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022·青岛模拟)
1. （1）化简： $\text{[math]}$ ；
2. （2）已知二次函数 $\text{[math]}$ 与正比例函数 $\text{[math]}$ 的图象只有一个交点，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2022·青岛模拟) 小明和小亮做游戏，规则如下：将正面分别写有数字1，2，3，4的4张卡片背面朝上，洗匀．先从中任意抽取1张（不放回），再从余下的3张中任意抽取1张，若抽得的2张卡片上的数字之和为2的倍数则小明胜，若抽得的2张卡片上的数字之和为3的倍数则小亮胜．这个游戏对双方公平吗？请说明理由．

答案解析收藏纠错 + 选题
18. (2022·青岛模拟) 如图，在港口A处的正东方向有两个相距 $\text{[math]}$ 的观测点B、C，一艘轮船从A处出发，北偏东 $\text{[math]}$ 方向航行至D处，在B、C处分别测得 $\text{[math]}$ ， $\text{[math]}$ 求轮船航行的距离AD (参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
19. (2022·青岛模拟) 某校为了解学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
①七年级成绩在 $\text{[math]}$ 这一组的是：70，72，74，75，76，76，77，77，77，78，79；
②七年级成绩频数分布直方图及七、八年级成绩的平均数、中位数分别如下：
年级
平均数
中位数
七
76.9
$\text{[math]}$
八
79.2
79.5
根据以上信息，回答下列问题：
1. （1）在这次测试中，七年级在80分以上（含80分）的有人；
2. （2）表中m的值为；
3. （3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是78分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；
4. （4）该校七年级学生有500人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数．
答案解析收藏纠错 + 选题
20. (2023八下·睢宁期末) 如图，已知过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与直线 $\text{[math]}$ ： $\text{[math]}$ 相交于点 $\text{[math]}$ .
1. （1）求直线 $\text{[math]}$ 的解析式；
2. （2）求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
21. (2022·青岛模拟) 已知 $\text{[math]}$ 是等边三角形，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，过点 $\text{[math]}$ 平行于 $\text{[math]}$ 的直线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 是 $\text{[math]}$ 的中点，请判断四边形 $\text{[math]}$ 的形状，并说明理由．
答案解析收藏纠错 + 选题
22. (2022·青岛模拟) “童心迎六一，欢乐共成长”，某超市计划在儿童节期间进行一款文具的促销活动．该文具进价为5元/件，售价为9元/件时，当天的销售量为100件．在销售过程中发现：售价每下降0.5元，当天的销售量就增加5件．设当天销售单价统一为 $\text{[math]}$ 元/件（ $\text{[math]}$ ，且 $\text{[math]}$ 是按0.5元的倍数下降），当天销售利润为 $\text{[math]}$ 元．
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；
2. （2）要使当天销售利润不低于240元，求当天销售单价所在的范围；
3. （3）若每件文具的利润不超过60%，要想当天获得最大利润，每件文具的售价应为多少元？并求出最大利润．
答案解析收藏纠错 + 选题
23. (2022·青岛模拟) 问题提出：把 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五个不同的棋子放在如图所示的 $\text{[math]}$ 方格纸内，使每行每列只能出现一个棋子，共有多少种不同的放法？
问题探究：为了解决上面的问题，我们先从最简单的情形入手，从中找到解决问题的方法．
探究一：
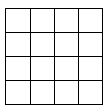
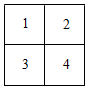
若把 $\text{[math]}$ ， $\text{[math]}$ 两个不同的棋子放在 $\text{[math]}$ 方格纸内，并使每行每列只能出现一个棋子，可看成分两步完成这件事情．第一步放棋子 $\text{[math]}$ ，棋子 $\text{[math]}$ 可以放在4个方格的任意一个中，故棋子 $\text{[math]}$ 有4种不同的放法．第二步放棋子 $\text{[math]}$ ，由于棋子 $\text{[math]}$ 已放定，那么放棋子 $\text{[math]}$ 的那一行和那一列中的其他方格内也不能放棋子 $\text{[math]}$ ，故还剩下1个方格可以放棋子 $\text{[math]}$ ，棋子 $\text{[math]}$ 只有1种放法．如：棋子 $\text{[math]}$ 放在方格1中，那么方格2和方格3也不能放棋子 $\text{[math]}$ ，棋子 $\text{[math]}$ 只能放在方格4中．由于第一步有4种放法，第二步有1种放法，所以共有 $\text{[math]}$ 种不同放法．
探究二：
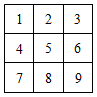
若把 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个不同的模子放在 $\text{[math]}$ 方格纸内，并使每行每列只能出现一个棋子，可看成分三步完成这件事情．第一步放棋子 $\text{[math]}$ ，棋子 $\text{[math]}$ 可以放在9个方格的任意一个中，故棋子 $\text{[math]}$ 有9种不同的放法．第二步放棋子 $\text{[math]}$ ，由于棋子 $\text{[math]}$ 已放定，那么放棋子 $\text{[math]}$ 的那一行和那一列中的其他方格内也不能放棋子 $\text{[math]}$ ，此时只剩四个方格可以放棋子 $\text{[math]}$ ，且四个方格的位置可类似看作“ $\text{[math]}$ 方格”模型，所以接下来放棋子 $\text{[math]}$ 和棋子 $\text{[math]}$ 的两步有 $\text{[math]}$ 种不同的放法．由于第一步有9种放法，第二步和第三步有 $\text{[math]}$ 种放法，所以共有 $\text{[math]}$ 种不同的放法．
1. （1）探究三：
  若把 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四个不同的棋子放在 $\text{[math]}$ 方格纸内，可看成分四步完成这件事情．第一步放棋子 $\text{[math]}$ ，棋子 $\text{[math]}$ 可以放在个方格的任意一个中，故棋子 $\text{[math]}$ 有种不同的放法．第二步放棋子 $\text{[math]}$ ，由于棋子 $\text{[math]}$ 已放定，那么放棋子 $\text{[math]}$ 的那一行和那一列中的其他方格内也不能放棋子 $\text{[math]}$ ，此时只有个方格可以放棋子 $\text{[math]}$ ，且这些方格的位置可类似看作“方格”模型，所以接下来放棋子 $\text{[math]}$ ，棋子 $\text{[math]}$ 和棋子 $\text{[math]}$ 的三步有种不同的放法．所以共有种不同的放法．
2. （2）问题解决：把 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五个不同的棋子放在 $\text{[math]}$ 方格纸内，并使每行每列只能出现一个棋子，共有种不同的放法．
3. （3）拓展延伸：若安排甲，乙，丙，丁，戊五人分别坐在五个不同的位置上，共有种不同的坐法．
答案解析收藏纠错 + 选题
24. (2022·青岛模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点．点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向匀速运动，速度为1cm/s；同时，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．设运动时间为 $\text{[math]}$ ，请解答下列问题：
1. （1）当 $\text{[math]}$ 为何值时， $\text{[math]}$ 是直角三角形？
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ ，设四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，试确定 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；
3. （3）当 $\text{[math]}$ 为何值时，四边形 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积相等？
4. （4）在运动过程中，是否存在某一时刻 $\text{[math]}$ ，使 $\text{[math]}$ 平分 $\text{[math]}$ ？若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题