陕西省西安市蓝田县2022年九年级中考二模数学试卷

更新时间：2024-07-13 浏览次数：64 类型：中考模拟

一、单选题

1. (2022七下·路北期中) 下列各数中，立方根不等于它本身的是（）

A . 2 B . 1 C . 0 D . －1

答案解析收藏纠错 + 选题
2. (2022·蓝田模拟) 长城被誉为“世界中古七大奇迹之一”，它的全长超过21000千米，数据21000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·蓝田模拟) 如图，在第24届北京冬奥会的口号“一起向未来”五个字及会徽被分开印刷在一个正方体的六个面上，其平面展开图如图所示，那么在该正方体中与北京冬奥会会徽相对的面上的字是（）

A . 一 B . 起 C . 向 D . 未

答案解析收藏纠错 + 选题
4. (2022·蓝田模拟) 当光线从空气中射入某种液体中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射.如图， $\text{[math]}$ 液面MN于点D，一束光线沿CD射入液面，在点D处发生折射，折射光线为DE，点F为CD的延长线上一点，若入射角 $\text{[math]}$ ，折射角 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 14° B . 16° C . 18° D . 25°

答案解析收藏纠错 + 选题
5. (2022·蓝田模拟) 在如图所示的正方形网格中，每个小正方形的边长均为1， $\text{[math]}$ ABC的顶点A、B、C均在格点上，BD是AC边上的中线，则BD的长为（）

A . $\text{[math]}$ B . 1.5 C . $\text{[math]}$ D . 2.5

答案解析收藏纠错 + 选题
6. (2022八下·承德期末) 已知一次函数 $\text{[math]}$ ，函数值y随自变量x的增大而减小，且 $\text{[math]}$ ，则函数 $\text{[math]}$ 的图象经过的象限是（）

A . 第一、二、三象限 B . 第一、三、四象限 C . 第一、二、四象限 D . 第二、三、四象限

答案解析收藏纠错 + 选题
7. (2022·蓝田模拟) 如图，在菱形ABCD中， $\text{[math]}$ ，点P为边AB上一点（点P不与端点重合），连接CP，点E、F分别为AP、CP的中点，连接EF，若 $\text{[math]}$ ，则菱形ABCD的面积为（）

A . 8 B . $\text{[math]}$ C . 9 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·蓝田模拟) 已知抛物线 $\text{[math]}$ $\text{[math]}$ 是由抛物线 $\text{[math]}$ 向左平移2个单位得到，若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在抛物线 $\text{[math]}$ 上，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2022·蓝田模拟) 请写出一个比 $\text{[math]}$ 小的正整数．

答案解析收藏纠错 + 选题
10. (2022·蓝田模拟) 若一个正多边形的半径与它的边长相等，则过该正多边形的一个顶点的对角线有条.

答案解析收藏纠错 + 选题
11. (2022·蓝田模拟) 有一数值转换器，原理如图所示，若开始输入x的值是1，可发现第一次输出的结果是4，第二次输出的结果是2，……，请你探索第2021次输出的结果是.

答案解析收藏纠错 + 选题
12. (2022·蓝田模拟) 如图，点A为反比例函数 $\text{[math]}$ 的图象上一点，过点A作 $\text{[math]}$ 轴于点B，作 $\text{[math]}$ 轴于点D，反比例函数 $\text{[math]}$ 的图象与AB交于点C，连接OA、OC，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
13. (2022·蓝田模拟) 如图，点E、F为平行四边形ABCD的边BC上两点，且 $\text{[math]}$ ，连接DE、AF，DE与AF相交于点P，连接PB、PC，若 $\text{[math]}$ PAB与 $\text{[math]}$ PCD的面积之和为30，则 $\text{[math]}$ PBE与 $\text{[math]}$ PCF的面积之和为.

答案解析收藏纠错 + 选题

三、解答题

14. (2022·蓝田模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2022·蓝田模拟) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022·蓝田模拟) 解不等式 $\text{[math]}$ ，并将其解集表示在如图所示的数轴上.

答案解析收藏纠错 + 选题
17. (2022·蓝田模拟) 如图，点C为 $\text{[math]}$ 的边OA上一点， $\text{[math]}$ 于点D，请用尺规作图法在 $\text{[math]}$ 的内部作射线CE，使得 $\text{[math]}$ .（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
18. (2022·蓝田模拟) 如图，在平行四边形ABCD中，对角线AC与BD交于点O，且AC=BD，请你从①AC⊥BD、②AB=BC、③BD平分∠ABC中任选一个作为添加条件，另两个中的一个作为结论，组成一个真命题，并证明.
1. （1）添加条件：，结论：；（填序号）
2. （2）根据你所选择的条件和结论，写出证明过程.
答案解析收藏纠错 + 选题
19. (2023七下·凤台期末) 《孙子算经》是我国古代重要的数学著作，其中有如下问题：今有人盗库绢，不知所失几何，但闻草中分绢，人得六匹，盈六匹；人得七匹，不足七匹.问人、绢各几何？大意是：有几个盗贼偷了仓库里的绢，不知道具体偷盗了多少匹绢，只听盗贼在草丛中分绢时说：“每人分6匹，会剩下6匹；每人分7匹，还差7匹.”问有多少盗贼？多少匹绢？

答案解析收藏纠错 + 选题
20. (2022·蓝田模拟) 冰墩墩是2022年北京冬季奥运会的吉祥物，憨态可掬的外貌加上富有超能力的冰晶外壳，深受广大民众的喜爱.某商场为促进消费，举行了“玩转盘游戏，领奥运礼品”的促销活动，活动规定：将一个可自由转动的转盘平均分成4个扇形，如图，每个扇形中都有一个问题，顾客在该商场一次性消费每满300元，即可获得一次转转盘的机会.顾客转动一次转盘，转盘停止后，若将指针所指扇形中的问题回答正确，则可得到一个冰墩墩玩偶（若指针指在分界线上，则重转一次，直到指针指向某一个扇形区域为止）.已知小欣和妈妈在该商场消费600元，获得了两次转转盘机会.
1. （1）小欣转动一次转盘，转盘停止后指针指向扇形A的概率为；
2. （2）已知小欣只知道A、C两个问题的答案，请用列表法或画树状图的方法，求小欣转了两次转盘，至少得到一个冰墩墩玩偶的概率.
答案解析收藏纠错 + 选题

21. (2022·蓝田模拟) 九年级数学“综合与实践”课的任务是测量学校旗杆的高度.晓雪和她的朋友们制定了测量方案，并完成了实地测量，测量结果如下：

课题	测量学校旗杆的高度
测量工具	测角仪和皮尺
测量示意图及说明		说明：BC为水平地面，旗杆AB⊥BC，斜坡CD的坡度 $\text{[math]}$ ，在斜坡CD上的点E处，测得旗杆顶端A的仰角∠1的度数.
测量数据	BC=8米，CE=2 $\text{[math]}$ 米，∠1=50.3°
参考数据	$\text{[math]}$

请你根据以上测量结果，计算旗杆的高度AB.

答案解析收藏纠错 + 选题

22. (2022·蓝田模拟) 从黄土地上的村支书，到泱泱大国的领导人，习近平总书记始终保持劳动者本色，始终保持对劳动人民的深厚感情.总书记强调，“无论时代条件如何变化，我们始终都要崇尚劳动、尊重劳动者”.为强化劳动观念，弘扬劳动精神，某学校要求学生周末时间积极参加家务劳动，承担一定的家庭劳动，进一步培养生活自理能力和习惯，增强家庭责任意识.该学校为了解八年级同学们每周参加家务劳动时间的大致情况，从全校八年级学生中随机抽取部分学生，调查他们平均每周参加家务劳动的时间（单位：h），并对调查结果进行整理和分析，过程如下：

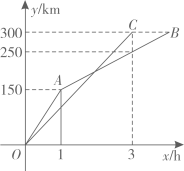
【收集数据】

1h	1.5h	1.5h	2h	2.5h	3h	3h	3.5h	4h	4h
4h	4.5h	5h	5h	5h	5h	5.5h	6h	6.5h	7.5h

【整理数据】

组别	A	B	C	D
时间x/h	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
人数/人	4	7	7	2

【分析数据】

平均数	中位数	众数
a	b	c

（1）填空：上表中a=，b=，c=；
（2）若该校共有500名八年级学生，请你估计其中平均每周参加家务劳动的时间不少于5h的学生有多少名？
（3）针对平均每周参加家务劳动的时间不足2h的学生，请你为他们提出一条合理化建议.

答案解析收藏纠错 + 选题

23. (2022·蓝田模拟) 近日，历经13年筹备与建设的全国首座考古学科专题博物馆——陕西考古博物馆正式建成，于4月28日至7月31日对外试行开放，它被网友称为是“中国文博又盛开的一朵美丽花朵”.五一期间，小明与晓慧两家从同一地点出发，沿同一路线分别驾车前往该博物馆参观，已知他们的出发地距离博物馆300km，图中折线 $\text{[math]}$ 、线段OC分别表示小明和晓慧距离出发地的路程 $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数关系，根据图象解答下列问题：
1. （1）求出发1小时后，小明距离出发地的路程 $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数关系式；
2. （2）小明和晓慧在途中相遇时，距离目的地还有多远？
答案解析收藏纠错 + 选题
24. (2022·蓝田模拟) 如图，在Rt $\text{[math]}$ ABC中， $\text{[math]}$ ，点O为BC上一点，以O为圆心、OB为半径的⊙ $\text{[math]}$ 切AC于点D，连接OA、BD、OA与BD相交于点E.
1. （1）求证：BD平分 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， ⊙ $\text{[math]}$ 的半径为10，求OE的长.
答案解析收藏纠错 + 选题
25. (2022·蓝田模拟) 在平面直角坐标系中，点O为坐标原点，经过点 $\text{[math]}$ 的抛物线 $\text{[math]}$ 与y轴交于点 $\text{[math]}$ ，直线l为该抛物线的对称轴，点B为点A关于对称轴l的对称点，连接AB、OB.
1. （1）试判断该抛物线与x轴交点的情况；
2. （2）点P为对称轴l左侧抛物线上的点，过点P作 $\text{[math]}$ 于点D，作 $\text{[math]}$ 轴于点C，连接CD，问是否存在点P，使得 $\text{[math]}$ PCD与 $\text{[math]}$ AOB相似？若存在，求出符合条件的点P的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
26. (2022·蓝田模拟)
1. （1）【问题提出】如图1，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E为AB延长线上一点，连接EC并延长，交AD的延长线于点F，则 $\text{[math]}$ 的度数为°；
2. （2）【问题探究】如图2，在Rt△ABC中， $\text{[math]}$ ，点D、E在直线BC上，连接AD、AE，若 $\text{[math]}$ ， $\text{[math]}$ ，求△ADE面积的最小值；
3. （3）【问题解决】近日，教育部印发了《义务教育课程方案和课程标准(2022年版)》，此次修订中增加的跨学科主题学习活动，突破学科边界，鼓励教师开展跨学科教研，设计出主题鲜明、问题真实的跨学科学习活动.为此，某校欲将校园内一片三角形空地ABC（如图3所示）进行扩建后作为跨学科主题学习活动中心，在AB的延长线上取一点D，连接DC并延长到点E，连接AE，已知 $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ ，为节约修建成本，需使修建后△ADE的面积尽可能小，问△ADE的面积是否存在最小值？若存在，求出其最小面积；若不存在，请说明理由.
答案解析收藏纠错 + 选题