天津市和平区2022年中考数学二模试题

更新时间：2024-07-13 浏览次数：107 类型：中考模拟

一、单选题

1. (2022·和平模拟) 计算﹣5﹣（﹣8）的结果等于（　　）

A . 3 B . 13 C . ﹣3 D . ﹣13

答案解析收藏纠错 + 选题
2. (2023·红桥模拟) 2tan45°的值等于（　　）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
3. (2022七上·阳信期末) 2021年5月15日，天问一号探测器成功着陆火星，中国成为全世界第二个实现火星着陆的国家．据测算，地球到火星的最近距离约为55 000 000km，将数据55 000 000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·和平模拟) 在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）

A . 稳 B . 中 C . 求 D . 进

答案解析收藏纠错 + 选题
5. (2022·和平模拟) 如图是一个由8个大小相同的小正方体组成的立体图形，它的左视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023七下·罗定期末) 估计 $\text{[math]}$ 的值在（　　）

A . 4和5之间 B . 5和6之间 C . 6和7之间 D . 7和8之间

答案解析收藏纠错 + 选题
7. (2022·和平模拟) 计算 $\text{[math]}$ 的结果是（　　）

A . 1 B . -1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七下·灌云月考) 已知二元一次方程组 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 2 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·和平模拟) 如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴上，顶点B，C的坐标分别为（﹣6，0），（4，0），则点D的坐标是（　　）

A . （6，8） B . （10，8） C . （8，6） D . （8，10）

答案解析收藏纠错 + 选题
10. (2022·和平模拟) 在反比例函数y＝ $\text{[math]}$ 的图象上有三点A（x₁ ， y₁），B（x₂ ， y₂），C（x₃ ， y₃），若x₁<0<x₂<x₃ ，则下列各式中正确的是（　　）

A . y₁＜y₃＜y₂ B . y₃＜y₂＜y₁ C . y₁＜y₂＜y₃ D . y₂＜y₁＜y₃

答案解析收藏纠错 + 选题
11. (2022·和平模拟) 如图，等腰直角△ABC中，AC=BC，∠ACB=90°，点D为斜边AB上一点，将△BCD绕点C逆时针旋转90°得到△ACE，对于下列说法不一定正确的是（　　）

A . ∠EAC＝∠B B . △EDC是等腰直角三角形 C . $\text{[math]}$ D . ∠AED=∠EDC

答案解析收藏纠错 + 选题
12. (2022·和平模拟) 如图，已知抛物线y＝ax²+bx+c（ $\text{[math]}$ 为常数，a≠0）的顶点为（1，n），抛物线与x轴交于点A（3，0），则下列结论：① $\text{[math]}$ ；②若方程ax²+bx+c﹣1=0的解是x₁ ， x₂ ，且满足x₁<x₂ ，则x₁<﹣1，x₂>3；③关于x的方程ax²+bx+c﹣n+1=0有两个不等的实数根；④ $\text{[math]}$ ．其中，正确的结论有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

13. (2022·和平模拟) 计算 $\text{[math]}$ 的结果等于．

答案解析收藏纠错 + 选题
14. (2022·津南模拟) 计算 $\text{[math]}$ 的结果等于．

答案解析收藏纠错 + 选题
15. (2022·和平模拟) 一个不透明的袋子里装有2个黄球、3个红球和5个黑球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是红球的概率是．

答案解析收藏纠错 + 选题
16. (2022·和平模拟) 直线y＝3x﹣2经过第象限，y随x的增大而，与x轴的交点坐标为．

答案解析收藏纠错 + 选题
17. (2022·和平模拟) 如图，已知∠AED＝∠ACB＝90°，AC=BC=3，AE=DE=1，点D在AB上，连接CE，点M，点N分别为BD，CE的中点，则MN的长为．

答案解析收藏纠错 + 选题

三、解答题

18. (2022·和平模拟) 如图，在每个小正方形的边长为1的网格中，△ABC的顶点A落在格点上，点B，点C均在网格线上，△ABC的外接圆交网格线于点D，△ABC的外接圆的圆心为O．
1. （1） BC为⊙O的；
2. （2） ⊙O上有一点P，连接DP，满足DP=AD，请在如图所示的网格中，用无刻度的直尺画出点P，并简要说明点P的位置是如何找到的（不要求证明）．
答案解析收藏纠错 + 选题
19. (2022·和平模拟) 解不等式组 $\text{[math]}$ 请结合题意填空，完成本题的解答．
1. （1）解不等式①，得；
2. （2）解不等式②，得；
3. （3）把不等式①和②的解集在数轴上表示出来：
4. （4）原不等式组的解集为．
答案解析收藏纠错 + 选题
20. (2022·和平模拟) 在疫情期间，学校推出了“空中课堂”，为了解该学校九年级学生每天听“空中课堂”的时间，随机调查了该校部分九年级学生，根据调查结果，绘制出如下的统计图①和图②．
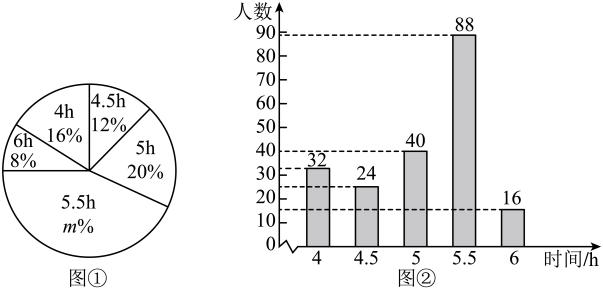
请根据相关信息，解答下列问题：
1. （1）参加这次调查的学生人数为；图①中m的值为；
2. （2）求统计的这组学生听课时间数据的平均数、众数和中位数；
3. （3）若该学校九年级共有800名学生，请估计该学校九年级学生每天听“空中课堂”的时间不低于5.5h的人数．
答案解析收藏纠错 + 选题
21. (2022·和平模拟) 如图，AB为⊙O直径，△ACD是⊙O的内接三角形，PB切⊙O于点B．
1. （1）如图①，延长AD交PB于点P，若∠C=40°，求∠P和∠BAP的度数；
2. （2）如图②，连接AP交⊙O于点E，若∠D=∠P，弧CE=弧AC，求∠P和∠BAP的度数．
答案解析收藏纠错 + 选题
22. (2022·和平模拟) 如图，斜立于地面的木杆AB，从点C处折断后，上半部分BC倒在地上，杆的顶部B恰好接触到地面D处，测得 $\text{[math]}$ ， $\text{[math]}$ ，折断部分CD长5.73米，求木杆AB的长度（结果保留整数）．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
23. (2022·和平模拟) 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
“低碳生活，绿色出行”的理念已深入人心，现在越来越多的人选择骑自行车出行，已知小红家，天塔，鼓楼在一条直线上，天塔离小红家2km，她从家骑自行车出发，匀速骑行0. 2小时后到达天塔，参观一段时间后按原速；匀速骑行前往鼓楼，刚到达鼓楼，接到妈妈电话，快速返回家中，回家途中匀速骑行．小红从家出发到返回家中，小红离开家的距离y km随离开家的时间x h变化的函数图象大致如图所示．
1. （1）填表：
  离开家的时间h
  0.1
  0.2
  0.5
  1.2
  离开家的距离y km
  2
2. （2）填空：
  ①小红在天塔游玩的时间为h；
  ②从天塔到鼓楼的途中，骑行速度为km/h；
  ③接到妈妈电话后，小红返回家的速度为km/h；
  ④小红离开家的距离为4km时，离开家的时间为h．
3. （3）当0. 8≤ x ≤1. 6时，请直接写出y关于x的函数解析式．
答案解析收藏纠错 + 选题
24. (2022·和平模拟) 将一个直角三角形纸片ABC放置在平面直角坐标系中，∠ACB=90°，点A(4， 0)，点C(0， 2)，点O(0，0)，点B在x轴负半轴，点E在线段AO上以每秒2个单位长度的速度从A向点O运动，过点E作直线EF⊥x轴，交线段AC于点F，设运动时间为t秒．将△AEF沿EF翻折，使点A落在x轴上点D处，得到△DEF．
1. （1）如图①，连接DC，当∠CDF=90°时，求点D的坐标．
2. （2） ①如图②，若折叠后△DEF与△ABC重叠部分为四边形，DF与边BC相交于点M，求点M的坐标（用含t的代数式表示），并直接写出t的取值范围；
  ②△DEF与△ABC重叠部分的面积为S，当 $\text{[math]}$ 时，求S的取值范围（直接写当出结果即可）．
答案解析收藏纠错 + 选题
25. (2022·和平模拟) 已知抛物线y＝ax²+bx+c（a，b，c为常数，a>0）经过A(-1，0)和B(3，0)两点，点C(0，-3)，连接BC，点Q为线段BC上的动点．
1. （1）若抛物线经过点C；
  ①求抛物线的解析式和顶点坐标；
  ②连接AC，过点Q作PQ∥AC交抛物线的第四象限部分于点P，连接PA，PB，AQ，△PAQ与△PBQ面积记为S₁ ， S₂ ，若S=S₁+S₂ ，当S最大时，求点P坐标；
2. （2）若抛物线与y轴交点为点H，线段AB上有一个动点G，AG=BQ，连接HG，AQ，当AQ+HG最小值为 $\text{[math]}$ 时，求抛物线解析式．
答案解析收藏纠错 + 选题