浙江省温州市乐清市2021-2022学年八年级下学期数学期末...

更新时间：2022-07-19 浏览次数：182 类型：期末考试

一、选择题（本题有10个小题，每小题3分，共30分．每小题只有一个正确选项，不选、多选、错选，均不给分）

1. (2022八下·乐清期末) 当a=5时，二次根式 $\text{[math]}$ 的值是（）

A . 3 B . 2 C . 1 D . -1

答案解析收藏纠错 + 选题
2. (2022八下·乐清期末) 下列图形是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022八下·乐清期末) 老师对甲、乙两位同学近六次数学测试成绩进行统计分析，已知甲的方差是2.2，甲的成绩比乙的成绩更稳定，则乙的方差可能是（）

A . 1.8 B . 2 C . 2.2 D . 3.2

答案解析收藏纠错 + 选题
4. (2024八下·柞水期末) 已知平行四边形的最小角为60°，则该平行四边形的最大角的度数是（）

A . 60° B . 120° C . 135° D . 150°

答案解析收藏纠错 + 选题
5. (2022八下·乐清期末) 把一元二次方程x（2x-1）=x-3化为一般形式，正确的是（）

A . 2x²+3=0 B . 2x²-2x-3=0 C . 2x²-x+2=0 D . 2x²-2x+3= 0

答案解析收藏纠错 + 选题
6. (2022八下·乐清期末) 已知正比例函数y=k₁x（k₁≠0）的图象与反比例函数y= $\text{[math]}$ （k₂≠0）的图象交于点A（-1，2），B（m，n），则点B的坐标是（）

A . （2，-1） B . （1，-2） C . （1，2） D . （-1，-2）

答案解析收藏纠错 + 选题
7. (2022八下·上城期中) 用反证法证明命题“在三角形中，至少有一个内角大于或等于60°“时，第一步应先假设（）

A . 三角形中有一个内角小于60° B . 三角形中有一个内角大于60° C . 三角形的三个内角都小于60° D . 三角形的三个内角都大于60°

答案解析收藏纠错 + 选题
8. (2022八下·乐清期末) 如图，在直角坐标系中，四边形ABCD是正方形，点A的坐标为（1，0），点B的坐标为（-1，4），点D在第一象限，则点C的坐标为（）

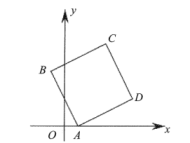
A . （3，6） B . （4，6） C . （4，5） D . （5，2）

答案解析收藏纠错 + 选题
9. (2022八下·乐清期末) 关于x的一元二次方程x²+4x+（1-m）（m-3）=0，下列选项正确的是（）

A . 没有实数根 B . 有两个相等的实数根 C . 有两个不相等的实数根 D . 根的个数与m的取值有关

答案解析收藏纠错 + 选题
10. (2022八下·乐清期末) 如图，线段AB与CD相交于点E，∠AED=45°，DE+AE=9，以AE和CE为边作 $\text{[math]}$ AGCE，以DE和BE为边作 $\text{[math]}$ EBFD，且 $\text{[math]}$ AGCE和 $\text{[math]}$ EBFD的面积都为3 $\text{[math]}$ ，若1<CE<3，则线段DF的取值范围是（）

A . $\text{[math]}$ <DF<2 B . $\text{[math]}$ <DF<2 C . $\text{[math]}$ <DF<3 D . 1<DF<3

答案解析收藏纠错 + 选题

二、填空题（本题有8个小题，每小题3分，共24分）

11. (2022八下·乐清期末) 四边形的外角和是度．

答案解析收藏纠错 + 选题
12. (2024八下·姜堰期末) 要使二次根式 $\text{[math]}$ 有意义，则x的值可以是（写出一个即可）

答案解析收藏纠错 + 选题
13. (2022八下·乐清期末) 某工厂第一季度的销售额为100万元，第三季度的销售额为169万元，设每季度平均增长率为x，则可列出方程为

答案解析收藏纠错 + 选题
14. (2022八下·乐清期末) 某校八年级一班举行投篮比赛，每人投3次球，右表记录了该班所有学生进球个数，从表中的数据得出所有学生进球数的中位数是个．

进球数

0个

1个

2个

3个

人数

2

12

9

7

答案解析收藏纠错 + 选题
15. (2022八下·乐清期末) 如图，在矩形ABCD中，E是AD边上的一点，且BC=BE，∠ABE=40°，则∠ECD= 度．

答案解析收藏纠错 + 选题
16. (2022八下·乐清期末) 已知关于x的一元二次方程 $\text{[math]}$ x²-x+m=0的一个根是-4，则该方程的另外一个根是

答案解析收藏纠错 + 选题
17. (2022八下·乐清期末) 如图，在反比例函数y= $\text{[math]}$ （常数k>0，x>0）图象上有点A，B，C，分别过这些点作x轴与y轴的垂线，交y轴于点D，E，F．若ED=EF=FO，且阴影部分面积为3，则k的值为

答案解析收藏纠错 + 选题
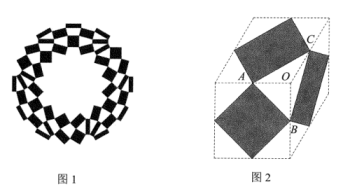
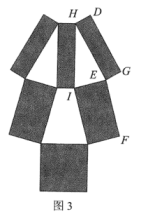
18. (2022八下·乐清期末) 如图1是第32届夏季奥运会的会徽，它是由三种不同规格的全等矩形组成，代表了不同的国家、文化和思维方式，表达了多样性的融合．图2和图3为该会徽中的某一部分。如图2，三种矩形分别由三种不同的菱形依次连结各边中点得到，其中∠AOC=120°，∠AOB=90°．如图3，点D恰好在FE的延长线上，则∠IHE= 度．若AO=1，则点F，G之间的距离为

答案解析收藏纠错 + 选题

三、解答题（本题有5小题，共46分解答时需要写出必要的文字说明、演算步骤或证明过程）

19. (2022八下·乐清期末)
1. （1）计算： $\text{[math]}$
2. （2）解方程：3（x-1）²=48．
答案解析收藏纠错 + 选题
20. (2022八下·乐清期末) 如图，在7×7的正方形网格中，每个小正方形的边长为1，线段AB的两个端点在网格的格点上，分别按下列要求画格点四边形（顶点均在格点上）．
1. （1）在图甲中画一个平行四边形ABCD，使得平行四边形ABCD的面积为12．
2. （2）在图乙中画一个四边形EABF，且EA不平行BF，使得四边形EABF的面积为12．
答案解析收藏纠错 + 选题
21. (2022八下·乐清期末) 在某校组织的数学知识竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，并且记A，B两个等级为优秀等级．学校将八年级一班和二班的成绩整理并绘制成如下的统计图．已知一班A等级的人数与二班D等级的人数相等．

请你根据以上提供的信息解答下列问题：
1. （1）求一班参加比赛总人数并补全一班竞赛成绩统计图．
2. （2）在平均数、众数、优秀率、中位数四个统计量中，选择一个适当的统计量，并借助数据说明哪一个班的竞赛成绩更优异？请阐述你的理由．
答案解析收藏纠错 + 选题
22. (2022八下·乐清期末) 如图，某校劳动小组计划利用已有的一堵长为6m的墙，用篱笆围成一个面积为12m²的矩形劳动基地ABCD，边AD的长不超过墙的长度，在BC边上开设宽为1m的门EF（门不需要篱笆）．设AB的长为x（m），BC的长为y（m）．
1. （1）求y关于x的函数表达式．
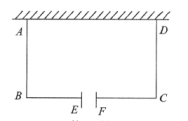
2. （2）若围成矩形劳动基地ABCD三边的篱笆总长为10m，求AB和BC的长度．
3. （3）若AB和BC的长都是整数（单位：m），且围成矩形劳动基地ABCD三边的篱笆总长小于10m，请直接写出所有满足条件的围建方案．
答案解析收藏纠错 + 选题
23. (2022八下·乐清期末) 点A是线段MN的中点，在MN同侧有B，D两点，连结AD，AB，∠DAM=∠BAN，DM∥BN，以AD，AB为边作 $\text{[math]}$ ABCD，分别延长BA与DM相交于点E，连结CA．
1. （1）求证：四边形EACD是平行四边形．
2. （2）已知MN=6，AC=3．
  ①若四边形ABCD是菱形，求菱形ABCD的周长．
  
  ②当AB=2AD时，则五边形DMNBC的面积为．（直接写出答案）
答案解析收藏纠错 + 选题