重庆市綦江区2021-2022学年八年级下学期期末数学试题

更新时间：2024-07-13 浏览次数：88 类型：期末考试

一、单选题

1. (2022八下·綦江期末) 下列各图给出了变量x与y之间的对应关系，其中y是x的函数的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022八下·綦江期末) 准备在甲，乙，丙，丁四人中选取成绩稳定的一名参加射击比赛，在相同条件下每人射击10次，已知他们的平均成绩相同，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则应该选择哪位运动员参赛（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
3. (2022八下·綦江期末) 下列二次根式中，属于最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022八下·靖西期末) 勾股定理是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中不能证明勾股定理的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022八下·綦江期末) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . 9 B . 8 C . 7 D . 6

答案解析收藏纠错 + 选题
6. (2022八下·綦江期末) 已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在直线 $\text{[math]}$ 上，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的值的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八下·綦江期末) 估计 $\text{[math]}$ -2的值在（）

A . 2到3之间 B . 3到4之间 C . 4到5之间 D . 5到6之间

答案解析收藏纠错 + 选题
8. (2023八下·滨海期中) 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A，B，C，D的边长分别是3、6、2、3，则最大正方形 $\text{[math]}$ 的面积是（）

A . 14 B . 34 C . 58 D . 72

答案解析收藏纠错 + 选题
9. (2022八下·綦江期末) 某校6名学生在2020年中考中的体育成绩（满分50分）统计如图所示，则这组数据的众数、中位数分别是（）

A . 50，48 B . 48，49 C . 50，49 D . 48，48

答案解析收藏纠错 + 选题
10. (2022八下·綦江期末) 下列说法中不正确的是（）

A . 对角线垂直的平行四边形是菱形 B . 对角线相等的平行四边形是矩形 C . 对角线互相垂直平分的四边形是正方形 D . 菱形的面积等于对角线乘积的一半

答案解析收藏纠错 + 选题
11. (2022八下·綦江期末) 如图，在平行四边形ABCD中，分别以AB、AD为边向外作等边△ABE和等边△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF、EF，则以下四个结论，正确的是（）
①△CDF≌△EBC；②∠CDF＝∠EAF；③CG⊥AE；④△CEF是等边三角形.

A . ③④ B . ①②④ C . ①②③ D . ①②③④

答案解析收藏纠错 + 选题
12. (2022八下·綦江期末) 若关于 $\text{[math]}$ 的一元一次不等式组 $\text{[math]}$ 恰有4个整数解，且一次函数 $\text{[math]}$ 不经过第三象限，则所有满足条件的整数 $\text{[math]}$ 的值之和是（）

A . -7 B . -12 C . -9 D . -11

答案解析收藏纠错 + 选题

二、填空题

13. (2022八下·綦江期末) 如图，两个正方形边长分别为 $\text{[math]}$ 、 $\text{[math]}$ ，图中阴影部分的面积为.

答案解析收藏纠错 + 选题
14. (2022八下·綦江期末) 实数 $\text{[math]}$ ， $\text{[math]}$ 在数轴上对应点的位置如图所示，化简 $\text{[math]}$ 的结果是.

答案解析收藏纠错 + 选题
15. (2022八下·綦江期末) 小南骑自行车从 $\text{[math]}$ 地向 $\text{[math]}$ 地出发，1小时后小通步行从 $\text{[math]}$ 地向 $\text{[math]}$ 地出发.如图，两条线段 $\text{[math]}$ 、 $\text{[math]}$ 分别表示小南、小通离 $\text{[math]}$ 地的距离y（单位：km）与所用时间x（单位：h）之间的函数图象，根据图中的信息，则小南、小通的速度分别是 km/ h， km/ h.

答案解析收藏纠错 + 选题
16. (2022八下·綦江期末) 重庆某大学对重庆某村实施“技术助农”.该村种植有A、B、C三种经济作物，助农前，A，B，C三种作物亩数比例为2：5：3；助农后，三种经济作物的亩数都得以增加，其中B作物增加的亩数占总增加亩数的 $\text{[math]}$ .助农前，C作物的亩产量是B作物亩产量的2.5倍，A，B两种作物的亩产量之和恰好是C作物的亩产量；助农后，A，B两种作物的亩产量分别增加了 $\text{[math]}$ 和 $\text{[math]}$ ， A，B两种作物的亩产量之和恰好仍是C作物的亩产量.若助农后，B作物的产量比助农前A，B产量之和多 $\text{[math]}$ ，而C作物的产量比助农前A，B，C三种作物产量的总和还多5%，则助农前后A作物的产量之比为.

答案解析收藏纠错 + 选题

三、解答题

17. (2022八下·綦江期末) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2022八下·綦江期末) 已知，如图，BD是菱形ABCD的对角线，∠CBD=76°.
1. （1）请用尺规作图法作线段AB的垂直平分线EF，垂足为点E，交AD于点F，连接BF；（不写作法，保留作图痕迹）
2. （2）在（1）的条件下，求∠DBF的度数.
答案解析收藏纠错 + 选题
19. (2022八下·綦江期末) 一个有进水管与出水管的容器，从某时刻开始3min内只进水不出水，在随后的9min内既进水又出水，每分种的进水量和出水量是两个常数，容器内的水量y(单位：L)与时间(单位：min)之间的关系如图所示.
1. （1）当0≤x≤3时，求y关于x的函数解析式；
2. （2）当3< x≤12时，求y关于x的函数解析式；
3. （3）求进水速度是出水速度的多少倍？
答案解析收藏纠错 + 选题

20. (2022八下·綦江期末) 为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作，向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识，市教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果，对学生进行了新型冠状病毒肺炎防控知识测试，德育处随机从七八两个年级各抽取20名学生的答卷成绩（单位：分）进行统计分析，过程如下：

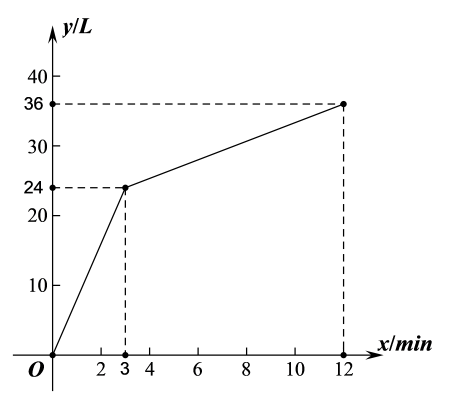
收集数据

八年级：

85	80	95	100	90	95	85	65	75	85
95	90	70	90	100	80	80	90	90	75

七年级：

70	70	80	95	70	100	90	75	80	70
95	100	80	80	100	80	95	100	95	90

整理数据

	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
八年级	2	5	8	5
七年级	4	6	2	8

分析数据

统计量	平均数（分）	中位数（分）	众数（分）
八年级	85.75	87.5	$\text{[math]}$
七年级	85.75	$\text{[math]}$	80

应用数据

（1）填空： $\text{[math]}$ （分）， $\text{[math]}$ （分）；
（2）在这次测试中，八年级学生甲与七年级学生乙的成绩都是86分，请判断两人在各自年级的排名谁更靠前，并说明理由.
（3）看完统计数据，你认为对新型冠状病毒肺炎防护知识掌握更好的是哪个年级？并说明理由.

答案解析收藏纠错 + 选题

21. (2022八下·綦江期末) 如图，有人在岸上点 $\text{[math]}$ 的地方，用绳子拉船靠岸，开始时，绳长 $\text{[math]}$ 米， $\text{[math]}$ 且 $\text{[math]}$ 米，拉动绳子将船从点 $\text{[math]}$ 沿 $\text{[math]}$ 方向行驶到点 $\text{[math]}$ 后，绳长 $\text{[math]}$ 米.
1. （1）试判定 $\text{[math]}$ 的形状，并说明理由；
2. （2）求船体移动距离 $\text{[math]}$ 的长度.
3. （3）若在BD段拉动船的速度为1米/秒，到达D后增加了人力，拉动船的速度变为2米/秒，求把船从B拉到岸边A点所用时间.
答案解析收藏纠错 + 选题
22. (2022八下·綦江期末) 如图，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$
1. （1）求直线 $\text{[math]}$ 的表达式；
2. （2）在直角坐标系中画出 $\text{[math]}$ 的图象，并求出该图象与直线 $\text{[math]}$ 及 $\text{[math]}$ 轴围成图形的面积；
3. （3）根据图象，直接写出关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集.
答案解析收藏纠错 + 选题
23. (2024八下·青山湖月考) 今年第6号台风“烟花”登录我国沿海地区，风力强，累计降雨量大，影响范围大，有极强的破坏力.如图，台风“烟花”中心沿东西方向AB由A向B移动，已知点C为一海港，且点C与直线AB上的两点A、B的距离分别为AC＝300km，BC＝400km，又AB＝500km，经测量，距离台风中心260km及以内的地区会受到影响.
1. （1）求∠ACB的度数；
2. （2）海港C受台风影响吗？为什么？
3. （3）若台风中心的移动速度为28千米/时，则台风影响该海港持续的时间有多长？
答案解析收藏纠错 + 选题
24. (2022八下·綦江期末) 对任意一个四位正整数m，如果m的百位数字等于个位数字与十位数字之和，m的千位数字等于十位数字的2倍与个位数字之和，那么称这个数m为“和谐数”.例如： $\text{[math]}$ ，满足 $\text{[math]}$ ， $\text{[math]}$ 所以5321是“和谐数”.例如： $\text{[math]}$ ，满足 $\text{[math]}$ ，但 $\text{[math]}$ 所以8523不是“和谐数”.
1. （1）判断5413和9588是不是“和谐数”，并说明理由；
2. （2）若m是“和谐数”，且m与23的和能被11整除，求满足条件的所有“和谐数”m.
答案解析收藏纠错 + 选题
25. (2022八下·綦江期末) 如图，在平行四边形ABCD中，点G是线段AB上一点，连接CG、DG，满足CG＝CD.
1. （1）如图1，过点G作GH⊥CD于点H，若AB＝8，GH＝2 $\text{[math]}$ ，求DG；
2. （2）如图2，若∠DAB＝60°，∠DAB的角平分线交CD于点E，过点E作EF∥AD，满足EF+AG＝AD，连接DF、CF，求证：∠DCF＝∠GCF.
3. （3）
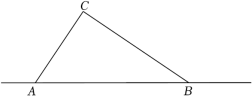
  拓展：如图，正方形ABCD的边长为4 $\text{[math]}$ ， E为BC上一点，且BE＝ $\text{[math]}$ ， F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，直接写出CG的最小值.
答案解析收藏纠错 + 选题