人教版物理八年级上册3.1温度同步练习

更新时间：2022-07-26 浏览次数：119 类型：同步测试

一、单选题

1. (2021八上·大化期末) 如图所示是实验室常用温度计和体温计，下列有关说法正确的是（）

A . 甲是体温计，乙是实验室常用温度计 B . 实验室常用温度计可以离开被测物体读数 C . 甲图所示温度计的读数为36℃ D . 甲、乙两种温度都是根据液体热胀冷缩原理制成的

答案解析收藏纠错 + 选题
2. (2021八上·宜州期末) 把一盆0℃的水放到-5℃的房间里，在水完全结成冰之前，这盆冰水的温度（）

A . 等于-5℃ B . 等于0℃ C . 介于0~-5℃之间 D . 无法确定

答案解析收藏纠错 + 选题
3. (2021八上·防城期末) 图所示的是一支常用体温计。下列关于该体温计的说法中，正确的是（）

A . 它的示数是8℃ B . 它的分度值是1℃ C . 它不能离开被测物体读数 D . 它是根据液体热胀冷缩的规律制成的

答案解析收藏纠错 + 选题
4. (2021八上·防城期末) 四位同学“用温度计测水温”的实验操作，如下图中所示，其中正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021八上·越秀期末) 贴片温度计常用在水族箱测试水温，制成此温度计是根据测温物质对温度敏感变色的规律，只要温度到达感温贴片的额定温度时，贴片就会开始变色，如此一来便能够提醒用户温度的变化，下图所示的是某贴片温度计的相关信息，你认为以下说法正确的是（）
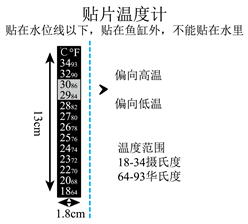
①此温度计是根据测温物质的热胀冷缩规律制成

②此温度计可以测出一标准大气压下的水的沸点

③可用此温度计准确判断某物体的温度为33.3℃

A . 只有①是正确的 B . 只有③是正确的 C . ①②③都是正确的 D . ①②③都是不正确的

答案解析收藏纠错 + 选题
6. (2021八上·会宁期末) 下列估测最符合实际情况的是（）

A . 人步行速度为10.8 km/h B . 全新的2B铅笔长约为18cm C . 人体感觉最舒适的温度是37℃ D . 一张考试卷厚度大约为1mm

答案解析收藏纠错 + 选题
7. (2021八上·深圳期末) 下列关于温度和温度计的说法正确的是（）

A . 0℃的冰比0℃的水冷 B . 正常情况下，人的体温约为25℃ C . 体温计内有一段弯曲的细管，防止水银流回玻璃泡 D . 体温计，酒精温度计都可离开被测物体进行读数

答案解析收藏纠错 + 选题
8. (2021八上·天河期末) 小明准备入口的热豆浆的温度约为（）

A . -16℃ B . 3℃ C . 40℃ D . 96℃

答案解析收藏纠错 + 选题
9. (2021八上·荔湾期末) 科学研究表明，无论采用什么方法降温，温度也只能非常接近 $\text{[math]}$ ，不可能达到该值或比它更低。若把 $\text{[math]}$ 定义为0“度”，每上升1度与上升 $\text{[math]}$ 是相同的（1“度”大小等于 $\text{[math]}$ 大小），则用这种新方法表示的“200度”是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021八上·揭西期末) 学校在预防新冠肺炎期间，要求对每位师生进行体温检测，下列说法正确的是（）

A . 体温计的量程是35℃-45℃ B . 体温计的分度值为1℃ C . 某同学的体温是36.8℃，该同学体温正常 D . 沸水的温度一定是100℃

答案解析收藏纠错 + 选题

二、填空题

11. (2022八上·廉江期末) 如图，在测量温度时，甲、乙、丙三位同学按图所示方法读数，正确的是，读数是 ℃。

答案解析收藏纠错 + 选题
12. (2021八上·浈江期末) 如图甲中，实验室温度计的使用方法正确的是，图乙中温度计的示数是 ℃，该示数（选填“高于”或“低于”）人体的正常体温。

答案解析收藏纠错 + 选题
13. (2021八上·方正期末) 请读出图甲中刻度尺所测的长度是cm ，图乙中温度计所测量的温度是℃。

答案解析收藏纠错 + 选题
14. (2021八上·钦北期末) 如图甲、乙温度计的示数分别是、。

答案解析收藏纠错 + 选题
15. (2021八上·岑溪期末) 如图中（选填“甲”或“乙”）是体温计，测量体温时，体温计（选填“可以”或“不可以”）离开人体读数。

答案解析收藏纠错 + 选题
16. (2022八上·新兴期末) 小强在用温度计测量烧杯中液体温度时读取了四次数据，每次读数时温度计的位置如图甲所示，其中正确的是．图乙、丙分别是测冰和水时的温度计示数，那么冰的温度是℃，水的温度是℃．

答案解析收藏纠错 + 选题
17. (2021八上·麦积期末) 液体温度计的原理是利用液体的的性质制成，如图所示该体温计的示数为 ℃。

答案解析收藏纠错 + 选题

三、作图题

18. (2021八上·合浦期中) 如图所示的仪器是实验室常用的温度计的一部分，此时它的示数为-32℃，请用铅笔在图中把温度计的液柱部分涂黑。

答案解析收藏纠错 + 选题

四、实验探究题

19. (2021八上·天河期末) 小明把两端开口的细玻璃管插入水中，发现管内的液面上升，待液面静止时，管内外液面高度差为h（下图）。他查资料得知同一根细玻璃管的h与水温t有关，他想探究管内外液面高度差h与水温t的定量关系，需要测出多组不同的h与t。请帮他设计实验方案：
1. （1）实验目的：；
2. （2）实验步骤（请补充剩余步骤，序号自行添加）：
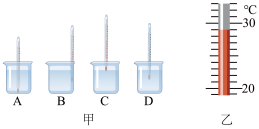
  ①按图所示，将玻璃管插入水中，待液面静止；
  ②用测出管内外液面高度差，记作h；
  ③；
  ④多次改变水温，用同一根细玻璃管重复上述步骤；
3. （3）设计记录数据的表格（将划线处补充完整，不需要填数据）。
  实验次数
  ①
  ②
  1
  2
  3
答案解析收藏纠错 + 选题

20. (2020八上·翼城期末) 学习《温度》后，老师组织同学们开展课外实践活动，利用身边的物品完成自制温度计的活动。如图甲所示是创新小组自制的温度计，瓶子作为玻璃泡装满某种液体，在密封的瓶塞上插上足够长的细管。为了探究薄壁细管内的液柱高度h与哪些因素有关，他们首先选用横截面积为S₁的细管进行实验，把玻璃泡浸没在不同温度的水中，如图乙所示，并将数据记录在表一中。然后换用横截面积为S₂的细管重复实验，将数据记录在表二中。（已知S₁>S₂）

表一：横截面积S₁

序号	温度t/℃	液柱高度h/cm	温度变化量 $\text{[math]}$ /℃	液柱高度的变化量 $\text{[math]}$ /cm
1	0	5	10	2
2	10	7	10	2
3	20	9	20	4
4	40	13	20	4
5	60	17	40	8
6	100	25	40	8

表二：横截面积S₂

序号	温度t/℃	液柱高度h/cm	温度变化量 $\text{[math]}$ /℃	液柱高度的变化量 $\text{[math]}$ /cm
7	0	6	5	1.5
8	5	7.5	5	1.5
9	10	9	20	6
10	30	15	20	6
11	60	24	30	9
12	90	33	30	9

（1）分析比较实验中（填写序号即可）几组数据及相关条件，可得出的初步结论是：同一玻璃泡，温度相同时，横截面积越小，液柱高度越大（说明：只写一组序号不得分）。
（2）分析比较表一（或表二）中液柱高度h和温度t的数据及相关条件，可得出的初步结论是：。
（3）该小组根据表一（或表二）中设计的项目还可以提出一个可探究性问题：。

答案解析收藏纠错 + 选题

21. (2020八上·永新期末) 疫情防控期间，小明是班级的卫生员，负责使用红外测温仪测量同学们的体温，在测量过程中发现同学们之间的体温相差较大，同一位同学连续三次体温测量值不相同。为了能够提高测量的精确度，小明提出猜想：体温的测量值可能与测温的部位、测量的距离有关。并进行了下面的探究活动：

（1）探究与测温部位的关系时，保持测温仪与人体的相同。对四位同学的额头与手腕分别进行了测量，数据记录如表1：

部位	t_甲/℃	t_乙/℃	t_丙/℃	t_丁/℃
额头	36.6	37.0	36.8	36.8
手腕	36.4	36.4	36.2	36.3

实验数据表明：体温的测量值与有关。

（2）探究与测温距离的关系时，保持相同，实验数据如表2：

间距（cm）	1	2	3	4	5	10	15	20	25	30
温度（℃）	36.5	36.5	36.5	36.4	36.3	36.1	35.7	35.1	34.7	34.1

由数据可知，在有效测温距离内，所测体温值与测温距离关（填“有”或“无”），测温距离大于有效测温距离，且测量距离越远，体温值（选填“变大”、“变小”）。

（3）根据实验结论，为了能够提高测量的精确度，小明建议用这种型号测温仪测量同学们的体温时，应该保持测温部位相同并保持测温相同，且有效测温距离在cm以内。

答案解析收藏纠错 + 选题

五、计算题

22. (2020八上·马鞍山期末) 小明自制了一支温度计，并运用等分原则为它做好了刻度。现在他用这支温度计与一支标准温度计一起测量两杯水温，所得数据如表：

第一杯

第二杯

自制温度计示数T/℃

14

50

标准温度计示数t/℃

10

50

这说明小明自制的温度计是一支不标准的温度计。
1. （1）若用此温度计测出的室温是23℃，实际室温是多少？
2. （2）写出T与t的关系式。
答案解析收藏纠错 + 选题
23. (2020八上·礼泉期末) 小明自制了一支粗细均匀的水银温度计，在标准大气压下用它分别测冰水混合物和沸水的温度时，温度计中液柱的长度分别为10cm、30cm，则：
1. （1）已知水银的熔点为-39℃，则该温度计（选填“能”或“不能”）准确测量零下50摄氏度的温度；
2. （2）所测物体温度每升高1℃，该温度计的液柱会伸长多少cm？
3. （3）液柱的长度为15cm时，所测物体的温度为多少℃？
答案解析收藏纠错 + 选题
24. (2020八上·蚌埠期中) 一支刻度均匀但示数不准确的温度计，在一个标准大气压下，放入冰水混合物中，它的示数为10℃，放入沸水中，它的示数为90℃，求：
1. （1）该温度计的示数为25℃时，实际温度是多少摄氏度？
2. （2）当实际温度为25℃时，此温度计的示数为多少摄氏度？
3. （3）若测某一液体温度时，温度计的示数恰好与实际温度相同，此时温度是多少摄氏度？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中