陕西省咸阳市咸阳彩虹学校2021-2022学年七年级下学期期...

更新时间：2024-07-31 浏览次数：78 类型：期中考试

一、单选题

1. (2022七下·咸阳期中) “碧玉妆成一树高，万条垂下绿丝绦”. 每到春天，人们流连于柳绿桃红之间的同时也被漫天飞舞的柳絮所烦扰.据测定，柳絮纤维的直径约为0.0000105m，该数值用科学记数法表示为（）

A . 1.05×10⁵ B . 1.05×10^－5 C . －1.05×10⁵ D . 105×10^－7

答案解析收藏纠错 + 选题
2. (2022七下·咸阳期中) 若∠1=25°，则∠1的余角的大小是（）

A . 55° B . 65° C . 75° D . 155°

答案解析收藏纠错 + 选题
3. (2022七下·咸阳期中) 下列计算正确的是（）

A . 6a⁸÷3a²=2a⁴ B . 2a（a-b）=2a²-b C . （a+1）（a-2）=a²-2 D . （-a-b）²=a²+2ab+b²

答案解析收藏纠错 + 选题
4. (2022七下·咸阳期中) 如图，小华同学的家在点P处，他想尽快到达公路边去接从外地回来的外婆，他选择沿线段PC去公路边，他的这一选择用到的数学知识是（）

A . 两点确定一条直线 B . 两点之间直线最短 C . 垂线段最短 D . 以上说法都不对

答案解析收藏纠错 + 选题
5. (2022七下·咸阳期中) 某河流遭受暴雨袭击，当天的水位记录如下表，观察表中数据，水位上升最快的时段是（）
时间/时
0
4
8
12
16
20
24
水位/m
2
2.5
3
4
5
6
8

A . 20~24时 B . 16~20时 C . 12~16时 D . 8~12时

答案解析收藏纠错 + 选题
6. (2022七下·咸阳期中) 直线 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 如图所示．若∠1=∠2，则下列结论错误的是（）

A . AB $\text{[math]}$ CD B . ∠EFB=∠3 C . ∠4=∠5 D . ∠3=∠5

答案解析收藏纠错 + 选题
7. (2022七下·咸阳期中) （ $\text{[math]}$ +m）与（ $\text{[math]}$ +3）的乘积中不含 $\text{[math]}$ 的一次项，则m的值为（）

A . -3 B . 3 C . 0 D . 1

答案解析收藏纠错 + 选题
8. (2022八下·射洪月考) 某天早晨，小明从家骑自行车去上学，途中因自行车发生故障而维修，如图所示的图象反映了他骑车上学的整个过程，则下列结论正确的是（）

A . 修车花了10分钟 B . 小明家距离学校1000米 C . 修好车后花了25分钟到达学校 D . 修好车后骑行的速度是110米/分钟

答案解析收藏纠错 + 选题

二、填空题

9. (2022七下·咸阳期中) 计算（a²b）³的结果是．

答案解析收藏纠错 + 选题
10. (2023七下·萧山期中) 已知直线a、b被直线c所截，则与∠1是内错角关系的是.

答案解析收藏纠错 + 选题
11. (2022七下·咸阳期中) 若一辆汽车以50km/h的速度匀速行驶，行驶的路程为s（km），行驶的时间为t（h），则用t表示s的关系式为．

答案解析收藏纠错 + 选题
12. (2022七下·咸阳期中) 计算799-801-800²=．

答案解析收藏纠错 + 选题
13. (2022七下·咸阳期中) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

14. (2022七下·咸阳期中) 计算：-4× $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2022八上·隆昌月考) 计算：（x+3）（x-7）-x（x-1）

答案解析收藏纠错 + 选题
16. (2023七下·界首期末) 如图，直线AB、CD相交于点O，OE把 $\text{[math]}$ 分成两部分，
1. （1）直接写出图中 $\text{[math]}$ 的对顶角为， $\text{[math]}$ 的邻补角为；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ =2：3，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
17. (2022七下·咸阳期中) 如图，在∠A中，B是AC边上一点，以B为顶点，BC为一边，利用尺规作图作∠EBC，使∠EBC=∠A；（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
18. (2022七下·咸阳期中) 小丽一天中的体温变化情况如图：
1. （1）大约什么时候，小丽的体温最低？最低体温约是多少？
2. （2）什么时间内，小丽的体温在升高？
3. （3）什么时间内，小丽的体温在保持不变？
答案解析收藏纠错 + 选题
19. (2022七下·咸阳期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2022七下·咸阳期中) 将下面的解答过程补充完整：已知：如图，直线AB，CD相交于点O，OE平分∠AOF，∠COE=90°．求证：∠FOB=2∠AOC．

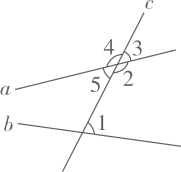
证明：因为OE平分∠AOF，所以∠AOE=∠EOF．（    ）

因为∠COE=90°，

所以∠AOC+∠AOE=90°

因为直线AB，CD相交于点O．

所以∠EOD=180°-∠COE=90°

所以．∠EOF+∠FOD=90°．

所以∠AOC= ．（    ）

因为直线AB，CD相交于O，

所以．（    ）

所以∠FOB=∠FOD+∠BOD=2∠AOC

答案解析收藏纠错 + 选题
21. (2023七下·兰州期中) 如图，梯形的上底长是5cm，下底长是13cm当梯形的高由大变小时，梯形的面积也随之发生变化．
1. （1）求梯形的面积y（cm²）与高x（cm）之间的表达式．
2. （2）当梯形的高由10cm变化到4cm时，则梯形的面积如何变化？
答案解析收藏纠错 + 选题
22. (2022七下·咸阳期中) 某学校教学楼前有一块长为 $\text{[math]}$ 米，宽为 $\text{[math]}$ 米的长方形空地要铺地砖，如图所示，空白的甲、乙两正方形区域是草坪，不需要铺地砖．两正方形区域的边长均为 $\text{[math]}$ 米．
1. （1）求铺设地砖的面积是多少平方米；
2. （2）当 $\text{[math]}$ ， $\text{[math]}$ 时，需要铺地砖的面积是多少？
答案解析收藏纠错 + 选题
23. (2022七下·咸阳期中) 如图，点P在直线CD上，AP与EF交于O点，∠AOE=∠1．∠FOP=∠2．
1. （1）若∠1=55°，求∠2的度数；
2. （2）若∠BAP+∠APD=180°试判断AE与FP的位置关系，并说明你的理由
答案解析收藏纠错 + 选题
24. (2022七下·咸阳期中) 在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，如表是测得的弹簧的长度y与所挂物体的质量x的几组对应值：
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
1. （1）上述表格反映了两个变量之间的关系，哪个是自变量？哪个是因变量？
2. （2）不挂物体时，弹簧长 cm；
3. （3）当所挂物体的质量为7kg时，弹簧的长度是多少？
4. （4）若弹簧的长度为34cm时，此时所挂重物的质量是多少？（在弹簧的允许范围内）
答案解析收藏纠错 + 选题
25. (2022七下·咸阳期中) 阅读材料：若满足（8-x）（x-6）=-3，求（8-x）²+（x-6）²的值．
解：设8-x=a，x-6=b，则（8-x）（x-6）=ab=-3，a+b=8-x+x-6=2
所以（8-x）²+（x-6）²=a²+b²=（a+b）²-2ab=2²-2×（-3）=10
请仿照上例解决下面的问题：
1. （1）问题发现：若x满足（3-x）（x-2）=-10，求（3-x）²+（x-2）²的值；
2. （2）若（6-x）²+（x-4）²=8求（6-x）（x-4）的值；
3. （3）类比探究：若x满足（2022-x）²+（2021-x）²=2020；求（2022-x）（2021-x）的值；
答案解析收藏纠错 + 选题
26. (2022七下·咸阳期中) 如图，已知AB $\text{[math]}$ CD， AD//BC，∠DCE=90°，点E在线段AB上，∠FCG=90°，点F 在直线AD上，∠AHG=90°．∠ECF=60°．
1. （1）找出一个角与∠D相等，并说明理由；
2. （2）如图，当点F在线段AD上时：
  ①写出一个与∠ADC相等的角 ▲ ；（写出一个即可）
  ②求∠BCD的度数；
3. （3）在点C运动过程中，点C （点C不与点B、H重合）从点B出发，沿射线BG的方向运动，其他条件不变，请求出∠BAF的度数．
答案解析收藏纠错 + 选题