锻炼时间/h | 5 | 6 | 7 | 8 |
人数 | 6 | 15 | 10 | 4 |
则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
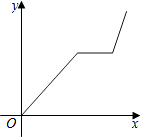 B .
B . 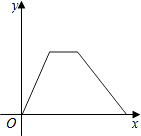 C .
C . 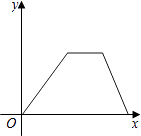 D .
D . 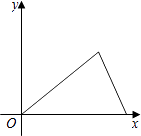


|
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
平均成绩 |
方差 |
|
|
甲 |
9 |
8 |
6 |
7 |
8 |
10 |
8 |
1.67 |
|
乙 |
8 |
7 |
8 |
9 |
9 |
7 |
8 |
0.67 |
甲和乙的训练成绩比较稳定的是.


时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
水量 | 0 | 1.5 | 3 | 4.5 | 6 | 8.5 | 9 |
在平面直角坐标系 中,点
到直线
的距离公式为:
,
例如,求点 到直线
的距离.
解:由直线 知:
所以 到直线
的距离为:
根据以上材料,解决下列问题:


组别 | 平均数(分) | 中位数(分) | 众数(分) |
七年级 | |||
八年级 |
阅读下列材料,完成相应任务.
直角三角形斜边上的中线等于斜边的一半
如图1,△ABC中,∠ABC=90°,BD是斜边AC上的中线.求证:BD=AC.
分析:要证明BD等于AC的一半.可以用“倍长法”将BD延长一倍,如图2,延长BD到E,使得DE=BD.连接AE,CE.可证四边形ABCE是矩形,由矩形的对角线相等得BE=AC,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到BD=AC.
